ОГЭ математика 2021. Разбор варианта Алекса Ларина № 257.

Решаем 257 вариант Ларина ОГЭ 2021 обычная версия. Подробное решение 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25 заданий обычного тренировочного варианта ОГЭ Ларина № 257 (alexlarin.com)
Аналоги к этому заданию: 
2247
2490
2511
689
910
409
539
80
100

Задание 1-5

Листы

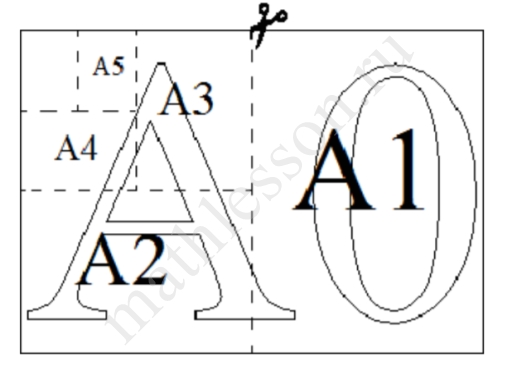
Общепринятые форматы листов бумаги обозначают буквой А и цифрой: А0, А1, А2 и так далее. Лист формата А0 имеет форму прямоугольника, площадь которого равна 1 кв. м. Если лист формата А0 разрезать пополам параллельно меньшей стороне, получается два равных листа формата А1. Если лист А1 разрезать так же пополам, получается два листа формата А2. И так далее. Отношение большей стороны к меньшей стороне листа каждого формата одно и то же, поэтому листы всех форматов подобны. Это сделано специально для того, чтобы пропорции текста и его расположение на листе сохранялись при уменьшении или увеличении шрифта при изменении формата листа.

1. В таблице даны размеры (с точностью до мм) четырёх листов, имеющих форматы А2, А4, А5 и А6.

Номер листа Длина, мм Ширина, мм
1 297 210
2 148 105
3 594 420
4 210 148

Установите соответствие между форматами и номерами листов. Заполните таблицу. В ответе запишите последовательность четырёх чисел без пробелов и других разделительных символов.

Формат А2 А4 А5 А6
Номер        

2. Сколько листов формата А3 получится из одного листа формата А1?

3. Найдите ширину листа бумаги формата А2. Ответ дайте в миллиметрах и округлите до ближайшего целого числа, кратного 10.

4. Найдите отношение длины меньшей стороны листа формата А5 к большей. Ответ округлите до десятых.

5. Размер (высота) типографского шрифта измеряется в пунктах. Один пункт равен $$\frac{1}{72}$$ дюйма, то есть 0,3528 мм. Текст напечатан шрифтом высотой 8 пунктов на листе формата А5. Какой высоты нужен шрифт (в пунктах), чтобы текст был расположен на листе формата А4 таким же образом? Размер шрифта округляется до целого.

Ответ: 1) 3142; 2) 4; 3) 420; 4) 0,7; 5) 11
Видео-решение Решение 1
ⓘ
Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

1. Расположим листы в порядке уменьшения длины: 594; 297; 210; 148. Тогда получим: 3142.

2. Из одного А1 получим 2 листа А2, аналогично из одного А2 два А3. Тогда из одного А1 получим 4 листа А3.

3. Ширина А2: 420 мм.

4. Отношение сторон для листов одинаково, потому возьмем А4: $$\frac{148}{210}\approx 0,704\approx 0,7$$.

5. Отношение длин А4 к А5: $$\frac{297}{210}$$. Тогда и отношение размеров шрифтов такое же. Следовательно, у А4: $$\frac{297}{210}\cdot 8\approx 11,3$$ пункта. Округлим: $$11,3\approx 11$$.

Аналоги к этому заданию: 
4209
1969
1310

Задание 6

Найдите значение выражения $$-\left(-0,4\right)\cdot \left(-0,1\right)\cdot \left(\frac{2}{3}-\frac{1}{2}\right)\cdot \frac{-1,5-3}{1,5-3}\cdot ({1,9}^2-1,9)$$

Ответ: -0,0342
Видео-решение Решение 1
ⓘ
Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$-\left(-0,4\right)\cdot \left(-0,1\right)\cdot \left(\frac{2}{3}-\frac{1}{2}\right)\cdot \frac{-1,5-3}{1,5-3}\cdot \left({1,9}^2-1,9\right)=$$ $$=-0,04\cdot \frac{1}{6}\cdot \frac{-4,5}{-1,5}\cdot 1,9\cdot 0,9\to -0,02\cdot 1,9\cdot 0,9=-0,0342.$$
Аналоги к этому заданию: 
2073
2103

Задание 7

Какое из данных ниже выражений тождественно равно выражению $$27^{\frac{2}{3}}$$?
1) $$9$$
2) $$18$$
3) $$40,5$$
4) $$243$$

Ответ: 1
Видео-решение Решение 1
ⓘ
Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$${27}^{\frac{2}{3}}={\left(3^3\right)}^{\frac{2}{3}}=3^2=9.\to 1$$ вариант ответа.

Задание 8

Найдите $$f(7)$$, если $$f(x^2 + 2x + 8) = 5^x$$.

Ответ: 0,2
Видео-решение Решение 1
ⓘ
Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$f\left(x^2+2x+8\right)=5^x:x^2+2x+8=7\leftrightarrow x^2+2x+1=0\leftrightarrow {\left(x+1\right)}^2=0\leftrightarrow x=-1$$ Тогда $$f\left(7\right)=5^{-1}=0,2$$.
Аналоги к этому заданию: 
4267
4385
2163

Задание 9

Стрелок три раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна $$0,8$$. Найдите вероятность того, что стрелок первые два раза попал в мишень, а последний раз промахнулся.

Ответ: 0,128
Видео-решение Решение 1
ⓘ
Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Вероятность промаха $$1-0,8=0,2$$. Тогда вероятность первыми двумя попасть, а потом промахнуться: $$0,8\cdot 0,8\cdot 0,2=0,128$$

Задание 10

Установите соответствие между графиками функций и функциями, соответствующими этим графикам. В ответе укажите последовательность цифр, соответствующих А, Б, В, без пробелов и других разделительных символов.

ГРАФИКИ

Формулы:
1) $$y = 2x^2 + 4x$$
2) $$y = -x^2 + 4x$$
3) $$y = -x^2 - 4x$$

А Б В
     
Ответ: 231
Видео-решение Решение 1
ⓘ
Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

1) $$y=2x^2+4x\to $$ нули функции $$2x^2+4x=0\leftrightarrow x=0;-2$$

2) $$-x^2+4x\to $$ нули функции $$-x^2+4x=0\leftrightarrow x=0;4$$

3) нули функции $$-x^2-4x=0\leftrightarrow x=0;-4$$

Тогда: 231.

Задание 11

Последовательность задана формулой $$c_n = \frac{47}{2n - 1}$$. Сколько членов этой последовательности больше 3?

Ответ: 8
Видео-решение Решение 1
ⓘ
Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$c_n>3\leftrightarrow \frac{47}{2n-1}>3\leftrightarrow \frac{47-6n+3}{2n-1}>0\leftrightarrow \frac{50-6n}{2n-1}>0\leftrightarrow \left\{ \begin{array}{c} n>\frac{1}{2} \\ n\frac{25}{3} \end{array} \right.$$ т.к. $$n\in N$$, то $$n=8$$ (максимум)

Задание 12

Центростремительное ускорение при движении по окружности (в м/с²) можно вычислить по формуле $$a = \omega^2 R$$, где $$\omega$$ — угловая скорость (в с⁻¹), а $$R$$ — радиус окружности. Пользуясь этой формулой, найдите расстояние $$R$$ (в метрах), если угловая скорость равна $$0,5$$ с⁻¹, а центростремительное ускорение равно $$1,75$$ м/с².

Ответ: 7
Видео-решение Решение 1
ⓘ
Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Подставим известные: $$1,75={0,5}^2R\to R=\frac{1,75}{0,25}=7$$.

Задание 13

Решите систему неравенств: $$\left\{\begin{aligned} x^2 \le 4 \\ x + 3 \ge 0 \end{aligned}\right.$$ В ответе укажите номер правильного ответа.
1) $$(-\infty; 3]$$
2) $$(-\infty; 3] \cup [2; +\infty)$$
3) $$[-2; 2]$$
4) $$[-2; 3]$$

Ответ: 3
Видео-решение Решение 1
ⓘ
Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

$${\rm \ }\left\{ \begin{array}{c} x^2\le 4 \\ x+3\ge 0 \end{array} \right.\leftrightarrow \left\{ \begin{array}{c} (x-2)(x+2)\le 0 \\ x\ge -3 \end{array} \right.\leftrightarrow \left\{ \begin{array}{c} x\ge -2 \\ x\le 2 \\ x\ge -3 \end{array} \right.\leftrightarrow x\in \left[-2;2\right],$$ т.е. 3 вариант.

Аналоги к этому заданию: 
4908
2323

Задание 14

В параллелограмме $$ABCD$$ диагональ $$AC$$ в $$2$$ раза больше стороны $$AB$$ и $$\angle ACD = 63^\circ$$. Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.

Ответ: 58,5
Видео-решение Решение 1
ⓘ
Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Пусть $$BD\cap AC=H\to AH=\frac{BD}{2}=AB\to \triangle ABH$$ - равнобедренный $$\to \ \angle ABH=\angle AHB=\frac{180{}^\circ -\angle BAH}{2}=\frac{180{}^\circ -63{}^\circ }{2}=58,5$$.

Задание 15

В треугольнике $$ABC$$ угол $$A$$ равен $$80^\circ$$, а угол $$B$$ равен $$40^\circ$$. Длина стороны $$AB$$ равна $$20\sqrt{3}$$. Найдите радиус окружности, описанной около треугольника $$ABC$$.

Ответ: 20
Видео-решение Решение 1
ⓘ
Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$\angle C=180{}^\circ -\left(\angle A+\angle B\right)=60{}^\circ . R=\frac{AB}{2{\sin C\ }}=\frac{20\sqrt{3}}{2\cdot \frac{\sqrt{3}}{2}}=20.$$

Задание 16

Основания трапеции равны $$6$$ и $$24$$, одна из боковых сторон равна $$11$$, а тангенс угла между ней и одним из оснований равен $$\frac{1}{\sqrt{35}}$$. Найдите площадь этой трапеции.

Ответ: 27,5
Видео-решение Решение 1
ⓘ
Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Пусть $$AB=11;\ {\tan A\ }=\frac{1}{\sqrt{35}}\to \frac{1}{35}+1=\frac{1}{{{\cos }^{{\rm 2}} A\ }}\to {{\cos }^{{\rm 2}} A\ }=\frac{35}{36}\to$$ $$\to {\cos A\ }=\frac{\sqrt{35}}{6}\to {\sin A\ }=\sqrt{1-{{\cos }^{{\rm 2}} A\ }}=\frac{1}{6}\to BH=AB{\sin A\ }=\frac{11}{6}$$. $$S_{ABCD}=\frac{6+24}{2}\cdot \frac{11}{6}=27,5$$

Задание 17

На клетчатой бумаге с размером клетки $$1 \times 1$$ изображён угол. Найдите тангенс этого угла.

Ответ: 1
Видео-решение Решение 1
ⓘ
Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Достроим треугольник $$ABC$$ и по теореме Пифагора найдем его стороны: видим, что $$AB^2+BC^2=AC^2\to \angle B=90{}^\circ \to {\tan BAC\ }=\frac{BC}{AB}=1$$

Задание 18

Какие из следующих утверждений верны? Если верных утверждений несколько, запишите их номера без пробелов и других разделительных символов в порядке возрастания.

  1. Окружность имеет бесконечно много центров симметрии.
  2. Правильный треугольник имеет центр симметрии.
  3. Правильный пятиугольник имеет пять осей симметрии.
Ответ: 2
Видео-решение Решение 1
ⓘ
Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$2.$$
Аналоги к этому заданию: 
2137

Задание 19

Решите систему неравенств: $$\left\{\begin{aligned} (6x + 2) - 6(x + 2) > 2x \\ (x - 7)(x + 6) 0 \end{aligned}\right.$$

Ответ: $$x\in (-6;-5).$$
Видео-решение Решение 1
ⓘ
Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$\left\{ \begin{array}{c} \left(6x+2\right)-6\left(x+2\right)>2x \\ \left(x-7\right)\left(x+6\right)0 \end{array} \right.\leftrightarrow \left\{ \begin{array}{c} 6x+2-6x-12-2x>0 \\ x>-7 \\ x6 \end{array} \right.\leftrightarrow$$ $$\leftrightarrow \left\{ \begin{array}{c} -10-2x>0 \\ x7 \\ x>-6 \end{array} \right.\leftrightarrow \left\{ \begin{array}{c} x-5 \\ x7 \\ x>6 \end{array} \right.\leftrightarrow x\in (-6;-5).$$

Задание 20

При каких значениях параметра $$a$$ прямая $$y = ax - 4$$ имеет с параболой $$y = x^2 + 3x$$ ровно одну общую точку? Постройте данные графики в одной системе координат.

Ответ: -1; 7
Видео-решение Решение 1
ⓘ
Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Приравняем функции: $$ax-4=x^2+3x\leftrightarrow x^2+x\left(3-a\right)+4=0$$. Раз одна общая точка, то решение одно, т.е. $$D=0$$: $${\left(3-a\right)}^2-4\cdot 4=0\leftrightarrow {\left(3-a\right)}^2=16\leftrightarrow \left[ \begin{array}{c} 3-a=4 \\ 3-a=-4 \end{array} \right.\leftrightarrow \left[ \begin{array}{c} a=-1 \\ a=7 \end{array} \right.$$.