ОГЭ математика 2021. Разбор варианта Алекса Ларина № 258.

Решаем 258 вариант Ларина ОГЭ 2021 обычная версия. Подробное решение 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25 заданий обычного тренировочного варианта ОГЭ Ларина № 258 (alexlarin.com)

Задание 1-5

Участок

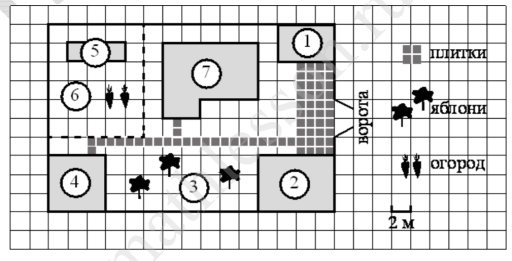
На плане изображён дачный участок по адресу: п. Сосновка, ул. Зелёная, д. 19 (сторона каждой клетки на плане равна 2 м). Участок имеет прямоугольную форму. Выезд и въезд осуществляются через единственные ворота.

При входе на участок слева от ворот находится гараж. Справа от ворот находится сарай площадью 24 кв. м, а чуть подальше — жилой дом. Напротив жилого дома расположены яблоневые посадки. Также на участке есть баня, к которой ведёт дорожка, выложенная плиткой, и огород с теплицей внутри (огород отмечен на плане цифрой 6).

Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1  м × 1  м. Между гаражом и сараем находится площадка, вымощенная такой же плиткой.

К участку подведено электричество. Имеется магистральное газоснабжение.

1) Для объектов, представленных в таблице, определите, какими числами они обозначены на плане. Заполните таблицу. В ответе запишите последовательность четырёх чисел без пробелов и других разделительных символов.

Объект Жилой дом Яблони Теплица Гараж
Число        

2) Тротуарная плитка продаётся в упаковках по 3 штуки. Сколько упаковок плитки понадобилось, чтобы выложить площадку между сараем и гаражом?

3) Найдите площадь, которую занимает баня. Ответ дайте в квадратных метрах.

4) На сколько процентов площадь, которую занимает гараж, больше площади, которую занимает теплица?

5) Хозяин участка решил покрасить весь забор вокруг участка (только с внешней стороны) в зелёный цвет. Площадь забора равна 232 кв. м, а купить краску можно в одном из двух ближайших магазинов. Цена и характеристика краски, а также стоимость доставки заказа даны в таблице.

  Магазин 1 Магазин 2
Расход краски (г/м2) 0,4 0,5
Масса краски в одной банке (кг) 4 3
Стоимость одной банки краски (руб.) 2200 1350
Стоимость доставки заказа (руб.) 800 900

Во сколько рублей обойдётся наиболее дешёвый вариант покупки с доставкой?

Ответ: 1) 7352; 2) 14; 3) 36; 4) 300; 5) 2250
Видео-решение Решение 1
ⓘ
Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

1) 2 - гараж

1 - сарай: $$S=2\cdot 3=6$$ клеток $$\to 1$$ клетка 4 м2 или сторона клетки 2 м.

4 - баня

5 - теплица, 6 - огород, 7 - дом, 3 - яблони

Тогда ответ: 7352

2) Количество плитки: $$5\cdot 2\cdot 4=40$$ шт.

Количество упаковок: $$n=\frac{40}{3}=13\frac{1}{3}\to 14$$ шт. 

3) Площадь бани: $$S=3\times 3=9$$ клеток или $$9\times 4=36$$ м2

4) Площадь гаража: $$3\times 4=12$$ клеток

Площадь теплицы: $$1\times 3=3$$ клетки

Пусть $$3-100%, 12-x%\to x=400%.$$ Тогда на $$300%$$ больше.

5) Магазин 1: $$232\cdot 0,4=92,8$$ гр. $$\to 1$$ банка $$\to 2200+800=3000$$ рублей.

Магазин 2: $$1350+900=2250$$ рублей

Задание 6

Найдите значение выражения $$\left(\frac{11}{13}-\frac{13}{11}\right):\left(\frac{11}{13}+\frac{13}{11}\right)\cdot \frac{{453}^2-{424}^2}{877}$$
Ответ: -4,8
Видео-решение Решение 1
ⓘ
Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$\left(\frac{11}{13}-\frac{13}{11}\right):\left(\frac{11}{13}+\frac{13}{11}\right)\cdot \frac{{453}^2-{424}^2}{877}=$$ $$=\frac{121-169}{11\cdot 13}\cdot \frac{11\cdot 13}{121+169}\cdot \frac{\left(453-424\right)\left(453+424\right)}{877}=-\frac{48}{290}\cdot \frac{29\cdot 877}{877}=-4,8.$$

Задание 7

Какое из данных ниже выражений тождественно равно выражению $$2^{\frac{6}{5}} \cdot 2^{\frac{9}{5}}$$? Варианты ответа:
1) $$\frac{25}{27}$$
2) $$1\frac{1}{3}$$
3) $$4\frac{8}{25}$$
4) $$8$$

Ответ: 4
Видео-решение Решение 1
ⓘ
Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$2^{\frac{6}{5}}\cdot 2^{\frac{9}{5}}=2^{\frac{6}{5}+\frac{9}{5}}=2^3=8\to $$ 4 вариант ответа.
Аналоги к этому заданию: 
2202
2459
2627

Задание 8

Найдите значение выражения $$\sqrt{17 - 12\sqrt{6 - 2\sqrt{5}} - 2\sqrt{5}}$$

Ответ: -3
Видео-решение Решение 1
ⓘ
Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$6-2\sqrt{5}=5-2\cdot 1\cdot \sqrt{5}+1={\left(\sqrt{5}-1\right)}^2.$$ Тогда: $$\sqrt{6-2\sqrt{5}}=\left|\sqrt{5}-1\right|=\sqrt{5}-1.$$ Получим: $$17-12\left(\sqrt{5}-1\right)=29-12\sqrt{5}.$$ При этом $$29-12\sqrt{5}=9-2\cdot 3\cdot 2\sqrt{5}+20={\left(3-2\sqrt{5}\right)}^2\to 29-12\sqrt{5}=$$ $$=\left|3-2\sqrt{5}\right|=2\sqrt{5}-3.$$ В итоге: $$2\sqrt{5}-3-2\sqrt{5}=-3$$

Задание 9

Решите уравнение: $$\frac{x - 3}{x + 2} + \frac{x + 2}{x - 3} = \frac{53}{14}$$. Если в уравнении более двух корней, запишите их без пробелов и других разделительных символов в порядке возрастания.

Ответ: -45
Видео-решение Решение 1
ⓘ
Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$\frac{x-3}{x+2}+\frac{x+2}{x-3}=\frac{53}{14}.$$ Пусть $$\frac{x-3}{x+2}=y,$$ тогда: $$t+\frac{1}{t}=\frac{53}{14}\to 14t^2-53t+14=0:D=2025\to $$ $$\to \left[ \begin{array}{c} t_1=\frac{53+45}{28} \\ t_2=\frac{53-45}{28} \end{array} \leftrightarrow \left[ \begin{array}{c} t_1=3,5 \\ t_2=\frac{2}{7} \end{array} \right.\right.\leftrightarrow \left[ \begin{array}{c} \frac{x-3}{x+2}=\frac{7}{2} \\ \frac{x-3}{x+2}=\frac{2}{7} \end{array} \right.\leftrightarrow \left[ \begin{array}{c} 2x-6=7x+14 \\ 7x-21=2x+4 \end{array} \right.\leftrightarrow$$ $$\leftrightarrow \left[ \begin{array}{c} x=-4 \\ x=5 \end{array} \right.$$
Аналоги к этому заданию: 
1924
422

Задание 10

В лыжных гонках участвуют $$11$$ спортсменов из России, $$6$$ — из Норвегии и $$3$$ — из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен из Норвегии или Швеции.

Ответ: 0,45
Видео-решение Решение 1
ⓘ
Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Для этого количество спортсменов из Норвегии и Швеции поделим на общее количество: $$P\left(A\right)=\frac{6+3}{20}=0,45.$$

Задание 11

Установите соответствие между графиками функций и функциями, соответствующими этим графикам. В ответе укажите последовательность цифр, соответствующих А, Б, В, без пробелов и других разделительных символов.

ГРАФИКИ

Формулы:
1) $$y = 2x^2 - 4x$$
2) $$y = -2x^2 - 4x$$
3) $$y = -2x^2 - 4x$$

А Б В
     
Ответ: 231
Видео-решение Решение 1
ⓘ
Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

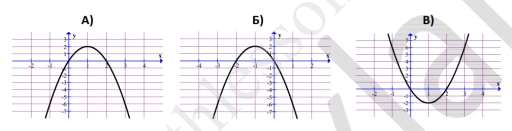
1) Нули функции: $$2x^2-4x=0\to x=0;2;$$ ветви вверх.

2) Нули: $$-2x^2+4x=0\to x=0;2;$$ ветви вниз $$\to 231$$

Аналоги к этому заданию: 
2196

Задание 12

Площадь параллелограмма $$S$$ (в м²) можно вычислить по формуле $$S = ab\sin \alpha$$, где $$a$$ и $$b$$ — стороны параллелограмма (в метрах). Пользуясь этой формулой, найдите площадь параллелограмма (в м²), если его стороны равны $$10$$ м и $$12$$ м, а $$\sin \alpha = 0,5$$.

Ответ: 60
Видео-решение Решение 1
ⓘ
Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$S=10\cdot 12\cdot 0,5=60$$
Аналоги к этому заданию: 
4919
2065

Задание 13

Решите неравенство $$\frac{x - 5}{4 - x} \ge 0$$. В ответе укажите номер правильного ответа:
1) $$[ 4;\ 5 ]$$
2) $$( 4;\ 5 ]$$
3) $$( -\infty;\ 4 ] \cup [ 5;\ +\infty )$$
4) $$( -\infty;\ 4 ) \cup [ 5;\ +\infty )$$

Ответ: 2
Видео-решение Решение 1
ⓘ
Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$\frac{x-5}{4-x}\ge 0\to \frac{x-5}{x-4}\le 0\leftrightarrow x\in (4;5]\to 2$$ вариант.

Задание 14

Последовательность задана формулой: $$c_n = n^2 - 1$$. Сколько членов этой последовательности больше $$200$$ и меньше $$500$$?

Ответ: 8
Видео-решение Решение 1
ⓘ
Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$\left\{ \begin{array}{c} n^2-1>200 \\ n^2-1500 \\ n\in N \end{array} \right.\leftrightarrow \left\{ \begin{array}{c} n^2>201 \\ n^2501 \\ n\in N \end{array} \right.\leftrightarrow \left\{ \begin{array}{c} n>\sqrt{201} \\ n\sqrt{501} \\ n\in N \end{array} \right.\leftrightarrow \left\{ \begin{array}{c} n\ge 15 \\ n\le 22 \\ n\in N \end{array} \right.\to 22-14=8.$$
Аналоги к этому заданию: 
2046
2544

Задание 15

Один из острых углов прямоугольного треугольника равен $$43^\circ$$. Найдите его другой острый угол. Ответ дайте в градусах.

Ответ: 47
Видео-решение Решение 1
ⓘ
Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$\alpha +\beta =90{}^\circ \to \alpha =90-\beta =90-43=47{}^\circ $$
Аналоги к этому заданию: 
1862
2301

Задание 16

На отрезке $$AB$$ выбрана точка $$C$$ так, что $$AC = 60$$, $$BC = 15$$. Построена окружность с центром $$A$$, проходящая через $$C$$. Найдите длину отрезка касательной, проведённой из точки $$B$$ к этой окружности.

Ответ: 30
Видео-решение Решение 1
ⓘ
Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Пусть M - точка касания, тогда: $$BM^2=BC\cdot BA\to BM=\sqrt{15\cdot 60}=15\cdot 2=30.$$

Задание 17

Сторона треугольника равна $$14$$, а высота, проведённая к этой стороне, равна $$23$$. Найдите площадь этого треугольника.

Ответ: 161
Видео-решение Решение 1
ⓘ
Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$S=\frac{1}{2}ah=\frac{1}{2}\cdot 14\cdot 23=161$$
Аналоги к этому заданию: 
2083
2156
2370

Задание 18

На клетчатой бумаге с размером клетки $$1 \times 1$$ изображён четырёхугольник. Найдите его площадь. Ответ дайте в квадратных сантиметрах.

Ответ: 9,5
Видео-решение Решение 1
ⓘ
Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$S=\frac{1}{2}\cdot 6\cdot 9-\frac{1}{2}\cdot 5\cdot 5-5\cdot 1=27-12,5-5=9,5$$

Задание 19

Какие из следующих утверждений верны? Если верных утверждений несколько, запишите их номера без пробелов и других разделительных символов в порядке возрастания.

  1. Диагональ параллелограмма делит его на два равных треугольника.
  2. Все углы ромба равны.
  3. Площадь квадрата равна произведению длин его двух смежных сторон.
Ответ: 13
Видео-решение Решение 1
ⓘ
Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$13$$
Аналоги к этому заданию: 
1748
2252

Задание 20

Решите систему неравенств: $$\left\{\begin{aligned} \frac{10 - 2x}{3 + (5 - 2x)^2} \ge 0 \\ 2 - 7x \le 14 - 3x \end{aligned}\right.$$

Ответ: $$x\in [-3;-5]$$
Видео-решение Решение 1 Решение 2
ⓘ
Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$\left\{ \begin{array}{c} \frac{10-2x}{3+{\left(5-2x\right)}^2}\ge 0 \\ 2-7x\le 14-3x \end{array} \right.\leftrightarrow \left\{ \begin{array}{c} 10-2x\ge 0 \\ -7x+3x\le 14-2 \end{array} \right.\leftrightarrow \left\{ \begin{array}{c} x\le 5 \\ -4x\le 12 \end{array} \right.\leftrightarrow$$ $$\leftrightarrow \left\{ \begin{array}{c} x\le 5 \\ x\ge -3 \end{array} \right.\leftrightarrow x\in [-3;-5]$$
Скрыть

Решите систему неравенств:

$$ \left\{ \begin{aligned} &\frac{10 - 2x}{3 + (5 - 2x)^2} \geq 0 \\ &2 - 7x \leq 14 - 3x \end{aligned} \right. $$

Решим первое неравенство:

$$ \frac{10 - 2x}{3 + (5 - 2x)^2} \geq 0 $$

Знаменатель всегда положителен, так как:

$$ 3 + (5 - 2x)^2 > 0 \quad \text{при любом } x $$

Значит, знак выражения зависит только от числителя:

$$ 10 - 2x \geq 0 \Rightarrow x \leq 5 $$

Решим второе неравенство:

$$ 2 - 7x \leq 14 - 3x $$ $$ 2 - 7x - 14 + 3x \leq 0 \Rightarrow -4x - 12 \leq 0 \Rightarrow -4x \leq 12 \Rightarrow x \geq -3 $$

Ответ:

$$ x \in [-3 \ ; \ 5] $$

Задание 21

Даша и Саша выполняют одинаковый тест. Дима отвечает за час на $$12$$ вопросов теста, а Саша - на $$22$$. Они одновременно начали отвечать на вопросы теста, и Дима закончил свой тест позже Саши на $$75$$ минут. Сколько вопросов содержит тест?

Ответ: 33
Видео-решение Решение 1
ⓘ
Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Пусть $$x$$ вопросов в тесте, тогда время Даши: $$\frac{x}{12}$$ часов, Саши: $$\frac{x}{22}$$ часов. Получим: $$\frac{x}{12}-\frac{x}{22}=\frac{75}{60}\leftrightarrow \frac{11x-6x}{2\cdot 6\cdot 11}=\frac{5}{4}\leftrightarrow x=33.$$

Задание 22

Постройте график функции $$y = \frac{x - 2}{2x - x^2}$$ и определите, при каких значениях $$k$$ прямая $$y = kx$$ имеет с графиком ровно одну общую точку.

Ответ: -0,25
Видео-решение Решение 1
ⓘ
Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$y=\frac{x-2}{2x-x^2}\leftrightarrow y=\frac{x-2}{x(2-x)}\leftrightarrow \left\{ \begin{array}{c} y=-\frac{1}{x} \\ x\ne 2 \end{array} \right.$$ $$y\left(2\right)=-\frac{1}{2}.$$ Одну точку будет иметь, если пройдет через $$\left(2;-\frac{1}{2}\right):$$ $$-\frac{1}{2}=k\cdot 2\to k=-0,25$$

Задание 23

Два равных прямоугольника $$ABCO$$ и $$KLMO$$ имеют общую вершину $$O$$, причём $$AO = OM$$ и $$OC = OK$$. Докажите, что площади треугольников $$AOK,\ COM$$ равны.

Ответ: ч.т.д.
Видео-решение Решение 1
ⓘ
Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

$$\angle AOK=\alpha \to \angle COM=360-2\cdot 90-\alpha =180-\alpha \to {\sin AOK\ }={\sin COM\ }.$$ $$S_{\triangle AOK}=\frac{AO\cdot OK\cdot {\sin AOK\ }}{2};\ S_{\triangle COM}=\frac{OC\cdot OM\cdot {\sin COM\ }}{2},$$ но $$AO=OM;OC=OK\to S_{AOK}=S_{COM}$$

Задание 24

Вершины ромба расположены на сторонах параллелограмма, а стороны ромба параллельны диагоналям параллелограмма. Найдите отношение площадей ромба и параллелограмма, если отношение для диагоналей параллелограмма равно $$54$$.

Ответ: $$\frac{108}{3025}$$
Видео-решение
ⓘ
Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!