ОГЭ математика 2023. Разбор варианта Алекса Ларина № 334.
Больше разборов на моем ютуб-канале
Задание 1-5
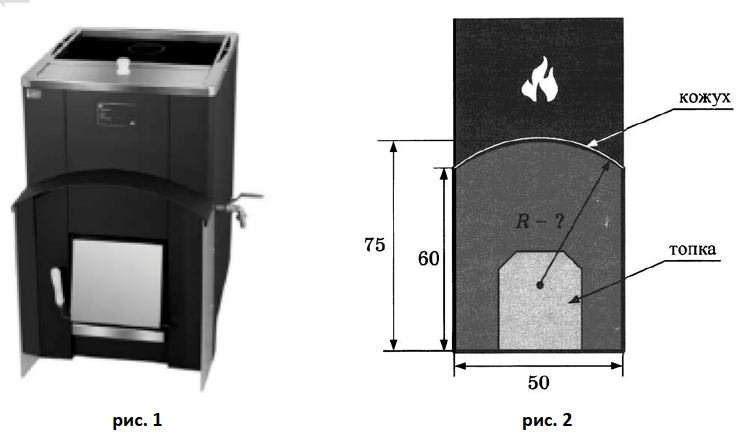
Печи
| Печь | Тип | Объём помещения (м3) | Масса (кг) | Стоимость (тыс. руб.) |
|---|---|---|---|---|
| Килиманджаро | дровяная | 4-8 | 45 | 14 |
| Кентавр | дровяная | 7-13 | 65 | 25 |
| Ока | электрическая | 8-14 | 14 | 23 |
Хозяин дачного участка строит баню с парным отделением. Парное отделение имеет размеры: длина 2,5 м, ширина 2,3 м, высота 2,1 м. Для прогрева парного отделения можно использовать электрическую или дровяную печь. В таблице (см. выше) представлены характеристики трёх печей.
Для установки дровяной печи дополнительных затрат не потребуется. Установка электрической печи потребует подведения специального кабеля, что обойдётся в 6 500 руб.
Кроме того, хозяин подсчитал, что за год электрическая печь израсходует 3000 киловатт-часов электроэнергии по 5 руб. за 1 киловатт-час, а дровяная печь за год израсходует 2 м3 дров, которые обойдутся по 1700 руб. за м3.
1. Найдите объём парного отделения строящейся бани (в м3).
2. На сколько рублей дровяная печь, подходящая по отапливаемому объёму парного отделения, обойдётся дешевле электрической с учётом установки?
3. На сколько рублей эксплуатация дровяной печи, которая подходит по отапливаемому объёму парного отопления, обойдётся дешевле эксплуатации электрической в течение года?
4. Доставка печи из магазина до участка стоит 500 руб. При покупке печи ценой выше 20 000 руб. магазин предлагает скидку 3% на товар и 35% на доставку. Сколько будет стоить покупка печи «Кентавр» вместе с доставкой на этих условиях?
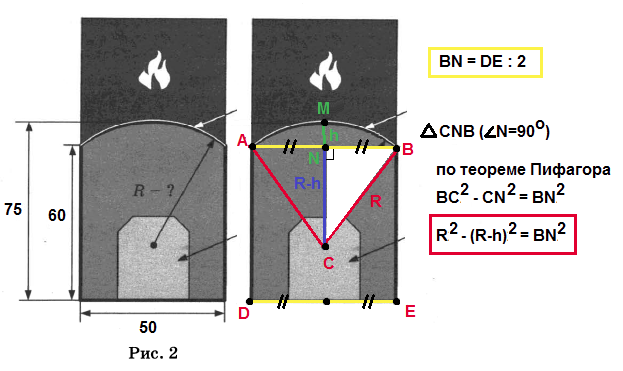
5. Печь снабжена кожухом вокруг дверцы топки. Верхняя часть кожуха выполнена в виде арки, приваренной к передней стенке по дуге окружности (см. рис. 2 выше). Для установки печки хозяину понадобилось узнать радиус закругления арки. Размеры кожуха показаны на рисунке. Найдите радиус в см. Результат округлите до десятых.
$$V = 2,5\cdot2,3\cdot2,1=12,075$$ м3
$$V = 2,5\cdot2,3\cdot2,1=12,075$$ м3
Килиманджаро (дровяная) - не подходит по объёму, отапливает до 12,075 м3
Кентавр (дровяная) - 25000 руб цена
Ока (электрическая) - 6500 установка + 23000 руб цена = 29500 руб
Дровяная печь дешевле электрической на $$29500-25000=4500$$ руб
$$V = 2,5\cdot2,3\cdot2,1=12,075$$ м3
Килиманджаро (дровяная) - не подходит по объёму, отапливает до 12,075 м3
Кентавр (дровяная) - $$2\cdot1700=3400$$ руб
Ока (электрическая) - $$3000\cdot5=15000$$ руб
Дешевле эксплуатация дровяной печи Кентавр на $$15000-3400=11600$$ руб
Кентавр (дровяная)
Цена 25000>20000, по условиям магазина:
Скидка на доставку товара $$35\% \Rightarrow$$ оплачиваем $$100\%-35\%=65\%$$
$$500\cdot0,65=325$$ руб
Скидка на товар $$3\% \Rightarrow$$ оплачиваем $$100\%-3\%=97\%$$
$$25000\cdot0,97=24250$$ руб
Стоимость дровяной печи = $$325+24250=24575$$ руб
Задание 6
Известно, что $$a 0 b 1$$. Какое из следующих утверждений относительно этих чисел является верным?
1) $$a^3 > 0$$
2) $$a - b > 0$$
3) $$ab 1$$
4) $$a + b > 1$$
В ответе запишите номер правильного варианта ответа.
Заметим, что $$-1<a<0, 0<b<1,$$ откуда $$a^3<0, a-b<0, ab<0, -1<a+b<1.$$ Таким образом, верным является утверждение $$ab<1.$$
Задание 7
Найдите значение выражения $$\frac{2^{n+2} \cdot 21^{n+3}}{6^{n+1} \cdot 7^{n+2}}$$.
$$\frac{2^{n+2}\cdot21^{n+3}}{6^{n+1}\cdot7^{n+2}}=\frac{2^n\cdot21^n\cdot2^2\cdot21^3}{6^n\cdot6^1\cdot7^n\cdot7^2}=\frac{42^n\cdot2^2\cdot3^3\cdot7^3}{42^n\cdot2\cdot3\cdot7^2}=2\cdot3^2\cdot7=14\cdot9=126$$
Задание 9
Найдите все такие значения $$x$$, при каждом из которых функция $$f(x)$$ принимает отрицательные значения. Установите соответствие между функциями и значениями $$x$$. В ответе запишите последовательность цифр, соответствующих А, Б, В, Г, без пробелов, запятых и других разделительных символов.
Функции:
A) $$f(x) = (x^2-2)(53x-75)$$
Б) $$f(x) = x^8 - x^5 + x^2 - x + 1$$
В) $$f(x) = x^2 + (x+2)^2 - \frac{60}{x^2+2x+3}$$
Г) $$f(x) = \frac{1}{x^2 + x} - \frac{1}{2x^2 + 2x + 3}$$
Ответы:
1) $$\varnothing$$
2) $$(-\infty;-\sqrt{2})\cup(\sqrt{2};+\infty)$$
3) $$(-3;1)$$
4) $$(-1;0)$$
| А | Б | В | Г |
А)
$$f(x)=0\Rightarrow\left[\begin{matrix} x^2-2=0\\ 53x-75=0 \end{matrix}\right.\Leftrightarrow x=\pm\sqrt{2}$$ и $$x=\frac{75}{53}$$
Очевидно, что это 2.
Б)
$$x^8-x^5+x^2-x+1=x^2(x^6+1)-x(x^6+1)+1=(x^6+1)(x^2-x)+1$$
При этом $$min(x^2-x)=(\frac{1}{2})^2-\frac{1}{2}=-\frac{1}{4}$$ и $$x^2-x=0$$ при $$x=0$$ и $$x=1.$$ При $$x\in(0;1)$$ имеем $$x^6+1\in(1;2)\Rightarrow (x^6+1)(x^2-x)$$ не выйдет за границы $$(2\cdot(-\frac{1}{4});1\cdot(-\frac{1}{4})),$$ т.е. $$(-\frac{1}{2};-\frac{1}{4})\Rightarrow$$ с учётом, что прибавляется 1, то выражение всегда положительное $$\Rightarrow 1$$ ответ.
Г)
Пусть $$x^2+x=y: \frac{1}{y}-\frac{1}{2y+3}<0\Rightarrow \frac{2y+3-y}{y(2y+3)}<0\Rightarrow \frac{y+3}{y(2y+3)}<0\Rightarrow$$
$$\Rightarrow y\in(-\infty;-3);(-\frac{3}{2};0).$$ Получим:
$$\left[\begin{matrix} x^2+x<-3\\ \left\{\begin{matrix} x^2+x>-\frac{3}{2}\\ x^2+x<0 \end{matrix}\right.\\ \end{matrix}\right.\Leftrightarrow\left[\begin{matrix} \varnothing\\ \left\{\begin{matrix} x\in R\\ x^2+x<0 \end{matrix}\right.\\ \end{matrix}\right.\Leftrightarrow x^2+x<0\Rightarrow x\in(-1;0)\Rightarrow 4$$ вариант.
Примечание от наборщика.
Ларин - чудак, такое детям в простом варианте не дают. Маразм крепчал.
Задание 10
Длину биссектрисы треугольника, проведённой к стороне $$a$$, можно вычислить по формуле $$l_a = \frac{2bc \cos\frac{\alpha}{2}}{b + c}$$. Вычислите $$\cos\frac{\alpha}{2}$$, если $$b = 1$$, $$c = 3$$, $$l_a = 1,2$$.
Выразим $$\cos\frac{\alpha}{2}$$ из данной формулы: $$\cos\frac{\alpha}{2}=\frac{l_{a}(b+c)}{2bc}$$. Найдем значение $$\cos\frac{\alpha}{2}=\frac{1,2(1+3)}{2*1*3}=0,8$$
Задание 11
Решите неравенство: $$(\sqrt{3} - 1,5)(3 - 2x) > 0$$
1) $$( -\infty;\ \frac{2}{3} )$$
2) $$( \frac{2}{3};\ +\infty )$$
3) $$( \frac{3}{2};\ +\infty )$$
4) $$( -\infty;\ \frac{3}{2} )$$
Можно поделить на первую скобку, так как больше нуля и знак неравенства не меняется:
$$3-2x>0$$
$$-2x>-3$$
$$2x>3$$
$$x<1,5\Rightarrow 4$$
Задание 12
Логично предположить, что в кладке с бревнами 12 рядов.
Пусть а1 = 1 - количество бревен в 1-ом ряду;
а12 = 12 - количество бревен в 12-ом ряду;
Знаменатель прогрессии d равен 1, т.к. количество бревен увеличивается на 1, если смотреть на ряды сверху вниз.
Нужна формула суммы первых n членов арифметической прогрессии.
$$S_n=\frac{(a_1+a_n)\cdot n}{2}=\frac{(1+12)\cdot12}{2}=78$$
Задание 13
Высота равностороннего треугольника равна $$59\sqrt{3}$$. Найдите его периметр.
Высота равностороннего треугольника равна $$\frac{a\sqrt{3}}{2}.$$
Следовательно, сторона треугольника $$a=59\sqrt{3}\cdot\frac{2}{\sqrt{3}}=118.$$
Тогда периметр равностороннего треугольника равен $$3\cdot118=354.$$
Задание 14
В окружность вписан равносторонний восьмиугольник $$ABCDEFGH$$. Найдите градусную меру угла $$ACE$$.
Равные хорды отсекают равные дуги. Т.е. каждая сторона отсекает дугу $$\frac{360^{\circ}}{8}=45^{\circ}.$$
$$\angle ACE$$ опирается на дугу, отсекаемую 4 сторонами, т.е. $$180^{\circ},$$ но угол вписанный $$\Rightarrow\angle ACE=\frac{180^{\circ}}{2}=90^{\circ}$$
Задание 15
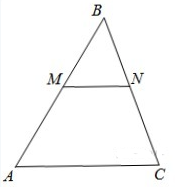
Прямая, параллельная стороне $$AC$$ треугольника $$ABC$$, пересекает стороны $$AB$$ и $$BC$$ в точках $$M$$ и $$N$$ соответственно, $$AC = 16$$, $$MN = 12$$. Площадь треугольника $$ABC$$ равна $$80$$. Найдите площадь треугольника $$MBN$$.
Треугольники MBN и АВС подобны, так как MN параллельна АС.
Из подобия:
$$\frac{MN}{AC}=\frac{12}{16}=\frac{3}{4}.$$ Это коэффициент подобия.
Площади подобных треугольников относятся как квадрат коэффициента подобия, то есть
$$\frac{S_{mbn}}{S_{abc}}=\frac{9}{16}.$$
Тогда $$S_{mbn}=\frac{9}{16}\cdot S_{abc}$$
$$S_{mbn}=\frac{9}{16}\cdot80=45$$
Задание 16
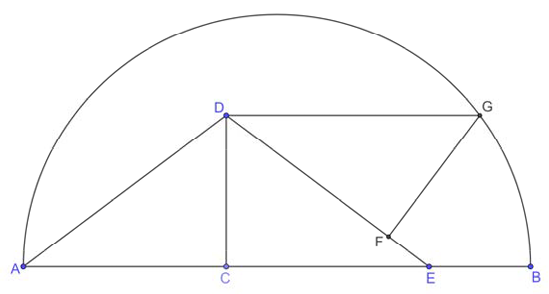
$$S=\frac{\pi R^2}{2}=\pi\cdot50\Rightarrow R^2=100\Rightarrow R=10\Rightarrow AB=20.$$
Опустим из G перпендикуляр на AB; пусть он пересекает $$AB=H.$$ Тогда $$AC=CE=x; EH=HB=y.$$
Или $$2x+2y=20\Rightarrow x+y=10.$$
Но DGHC - прямоугольник $$\Rightarrow DG=CH=x+y=10\Rightarrow DE=DG=10.$$
Задание 17
Какие из следующих утверждений верны? Если верных утверждений несколько, запишите их номера в порядке возрастания без пробелов, запятых и других разделительных символов.
- Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
- Треугольник со сторонами 1, 2, 4 существует.
- Если в ромбе один из углов равен $$90^{\circ}$$, то такой ромб — квадрат.
- Центр описанной около треугольника окружности всегда лежит внутри этого треугольника.
1) верно, через точку вне прямой можно провести параллельную этой прямой.
2) неверно, большая сторона треугольника должна быть меньше суммы двух других.
3) верно, т. к. если один из углов ромба равен 90°, то и остальные равны 90°.
4) неверно, есть тупоугольные треугольники, у которых центр описанной окружности вне его.
Задание 18
На области действительных значений $$x \in (-\infty; -3) \cup (-3; 0) \cup (0; +\infty)$$ упростите выражение: $$(\frac{x + 3}{x^2 - 3x} + \frac{x - 3}{x^2 + 3x}) \cdot \frac{9x - x^3}{x^2 + 9}$$
$$(\frac{x+3}{x^2-3x}+\frac{x-3}{x^2+3x})\cdot\frac{9x-x^3}{x^2+9}=\frac{(x+3)^2+(x-3)^2}{(x^2-9)x}\cdot\frac{x(9-x^2)}{x^2+9}=$$
$$=-\frac{x^2+6x+9+x^2-6x+9}{x^2+9}=-\frac{2(x^2+9)}{x^2+9}=-2$$
Задание 19
Расстояние между городами $$A$$ и $$B$$ равно $$750$$ км. Из города $$A$$ в город $$B$$ со скоростью $$50$$ км/ч выехал первый автомобиль, а через три часа после этого навстречу ему из города $$B$$ выехал со скоростью $$70$$ км/ч второй автомобиль. На каком расстоянии (в км) от города $$A$$ автомобили встретятся?
1) $$50\cdot3=150$$ (км) - прошел первый автомобиль до начала движения второго.
2) $$50 + 70 = 120$$ (км/ч) - скорость сближения автомобилей.
3) $$750 - 150 = 600$$ (км) - расстояние между автомобилями в момент начала движения второго.
4) $$\frac{600}{120} = 5$$ (ч) - двигались автомобили до встречи после выезда второго.
5) $$3 + 5 = 8$$ (ч) - затратил первый автомобиль до встречи со вторым.
6) $$50\cdot8 =400$$ (км) - на таком расстоянии от города а автомобили встретятся.
Задание 20
При каких значениях $$a$$ вершины парабол $$y = x^2 - 4ax + a$$ и $$y = -x^2 + 8ax + 4$$ расположены по одну сторону от оси $$x$$?
Для первой $$x_{0_1}=-\frac{-4a}{2}=2a,$$ для второй $$x_{0_2}=-\frac{8a}{-2}=4a$$
$$f(x_{0_1})=(2a)^2-4a\cdot2a+a=-4a^2+a$$
$$f(x_{0_2})=-(4a)^2+8a\cdot4a+4=16a^2+4$$
$$\left\{\begin{matrix} -4a^2+a>0\\ 16a^2+4>0 \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} -4a(a-\frac{1}{4})>0\\ a\in R \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} a(a-\frac{1}{4})<0\\ a\in R \end{matrix}\right.\Leftrightarrow a\in(0;\frac{1}{4})$$
Вариант, когда оба отрицательные, не имеет решений.
Задание 21
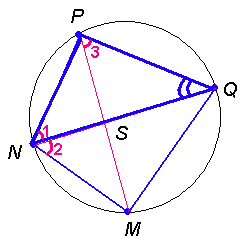
В выпуклом четырёхугольнике $$NPQM$$ диагональ $$NQ$$ является биссектрисой угла $$PNM$$ и пересекается с диагональю $$PM$$ в точке $$S$$. Найдите $$NS$$, если известно, что около четырёхугольника $$NPQM$$ можно описать окружность, $$PQ=86$$, $$SQ=43$$.
Задание 22
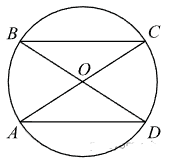
В окружности через середину $$O$$ хорды $$BD$$ проведена хорда $$AC$$ так, что дуги $$AB$$ и $$CD$$ равны. Докажите, что $$O$$ — середина хорды $$AC$$.