Задание 775
Задание 775
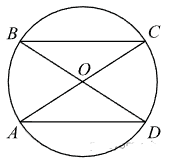
В окружности через середину $$O$$ хорды $$BD$$ проведена хорда $$AC$$ так, что дуги $$AB$$ и $$CD$$ равны. Докажите, что $$O$$ — середина хорды $$AC$$.
Вписанные углы ADB, CBD, ACB и DAC опираются на равные дуги, значит, они равны.
Получаем, что треугольники СOВ и AOD подобны по двум углам; их коэффициент подобия равен $$\frac{AO}{OC}$$
Поскольку AO = OC, эти треугольники равны, следовательно, AO = OC.
Аналоги к этому заданию:
Задание 3663
В окружности через середину $$O$$ хорды $$AC$$ проведена хорда $$BD$$ так, что дуги $$AB$$ и $$CD$$ равны. Докажите, что $$O$$ — середина хорды $$BD$$.
1) $$\angle BAC=\angle BDC$$ (вписанные и опираются на одну дугу)
2) $$AB=CD$$ (т.к. $$\smile AB=\smile CD$$); $$OA=OC$$ $$\Rightarrow$$ $$\bigtriangleup OAB=\bigtriangleup COD$$ (по двум сторонам и углу между ними) $$\Rightarrow$$ $$OB=OD$$