ОГЭ математика 2023. Разбор варианта Алекса Ларина № 340.
Больше разборов на моем ютуб-канале
Задание 1-5
Метро
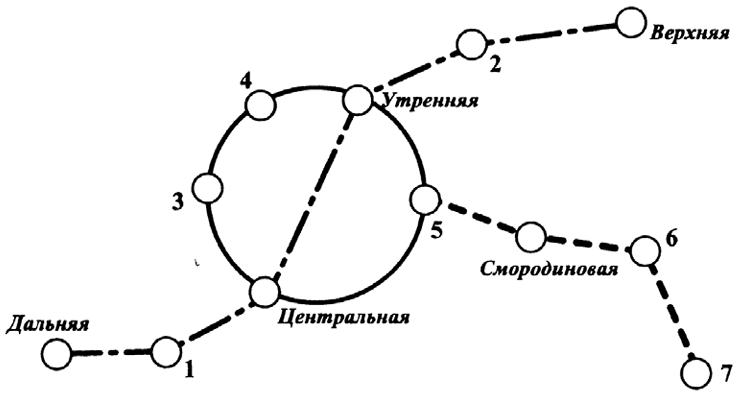
На рисунке (см. выше) изображена схема метро города N. Станция Ветреная расположена между станциями Центральная и Дальняя. Если ехать по кольцевой линии (она имеет форму окружности), то можно последовательно попасть на станции Центральная, Быстрая, Утренняя, Птичья и Весёлая. Радужная ветка включает в себя станции Быстрая, Смородиновая, Хоккейная и Звёздная. Всего в метрополитене города N есть три станции, от которых тоннель ведёт только в одну сторону - это станции Дальняя, Верхняя и Звёздная. Антон живёт недалеко от станции Надежда.
1. Для станций, указанных в таблице, определите, какими цифрами они обозначены на схеме. Заполните таблицу. В ответе запишите последовательность пяти цифр без пробелов, запятых и других разделительных символов.
| Станции | Весёлая | Ветреная | Звёздная | Птичья | Быстрая |
|---|---|---|---|---|---|
| Цифры |
2. Бригада меняет рельсы на участке между станциями Надежда и Верхняя протяжённостью 12,6 км. Работы начались в пятницу. Каждый рабочий день бригада меняла по 400 метров рельсов. По субботам и воскресеньям замена рельсов не осуществлялась, но проезд был закрыт до конца всего ремонта. Сколько дней был закрыт проезд между указанными станциями?
3. Территория, находящаяся внутри кольцевой линии, называется Центральным городским районом. Найдите его площадь $$S$$ (в км2), если длина кольцевой ветки равна 42 км. В ответе укажите значение выражения $$S\cdot\pi$$.
4. Найдите расстояние (в км) между станциями Смородиновая и Хоккейная, если длина Радужной ветки равна 17 км, расстояние от Звёздной до Смородиновой равно 12 км, а от Быстрой до Хоккейной - 15 км. Все расстояния даны по железной дороге.
5. Школьник Антон в среднем в месяц совершает 46 поездок в метро. Для оплаты поездок можно покупать различные карточки. Стоимость одной поездки для разных видов карточек различна. По истечении месяца Антон уедет из города и неиспользованные карточки обнуляются. Во сколько рублей обойдётся самый дешёвый вариант?
| Количество поездок | Стоимость карточки (руб.) | Дополнительные условия |
|---|---|---|
| 1 | 40 | школьникам скидка 15% |
| 10 | 370 | школьникам скидка 10% |
| 30 | 1050 | школьникам скидка 10% |
| 50 | 1500 | нет |
| Не ограничено | 2000 | нет |
Если ехать по кольцевой линии (она имеет форму окружности), то можно последовательно попасть на станции Центральная, Быстрая, Утренняя, Птичья и Весёлая. Значит, станция Птичья отмечена на схеме цифрой 4, а станция Весёлая цифрой 3. Станция Ветреная расположена между станциями Центральная и Дальняя, значит, станция Ветреная отмечена на схеме цифрой 1. Радужная ветка включает в себя станции Быстрая, Смородиновая, Хоккейная и Звёздная. Следовательно, станция Звёздная отмечена цифрой 7, а станция Быстрая цифрой 5.
$$\frac{12,6}{0,4}=31,5$$ дней. При этом каждые 5 дней добавляется ещё 2, то есть ещё 12 дней. Но так как работы начались в пятницу, то ещё +2 дня выходит.
Итого $$32+12+2=46$$ дней.
Сначала найдём радиус окружности:
$$R=\frac{L}{2\pi}=\frac{42}{2\pi}=\frac{21}{\pi}$$.
Теперь найдём площадь:
$$S=\pi R^2=\pi\cdot\frac{441}{\pi^2}=\frac{441}{\pi}$$.
Таким образом, получаем ответ:
$$S\cdot\pi=\frac{441}{\pi}\cdot\pi=441$$.
Расстояние от Звёздной до Хоккейной равняется $$17-15=2$$ км. Расстояние от Быстрой до Смородиновой равняется $$17-12=5$$ км. Значит, расстояние между станциями Смородиновая и Хоккейная равно $$17-2-5=10$$ км.
Самый дешёвый вариант 6 билетов по 40 и по абонементам на 10 и 30 поездок.
$$40\cdot6\cdot0,85+(370+1050)\cdot0,9=1482$$
Задание 8
Решите уравнение: $$(2x - 3)^2 = (2x - 1)^2$$. В ответе запишите корень этого уравнения.
$$\left[\begin{matrix} 2x-3=2x-1\\ 2x-3=-2x+1 \end{matrix}\right.\Leftrightarrow\left[\begin{matrix} -2=0\\ 4x=4 \end{matrix}\right.\Leftrightarrow\left[\begin{matrix} \varnothing\\ x=1 \end{matrix}\right.$$
Задание 9
Найдите все действительные значения $$x$$, при каждом из которых каждая из функций $$f(x)$$ и $$g(x)$$ лежит выше графика функции $$h(x)$$. Установите соответствие между функциями $$f(x),\; g(x),\; h(x)$$ и значениями $$x$$. В ответе запишите последовательность цифр, соответствующих А, Б, В, Г, без пробелов, запятых и других разделительных символов.
Функции:
A) $$f(x) = x^2 - 3x,\; g(x) = \frac{4-x}{2+x},\; h(x) = x$$
Б) $$f(x) = x^2 + 3x,\; g(x) = \frac{4+x}{2+x},\; h(x) = x+2$$
В) $$f(x) = \sqrt{x-2},\; g(x) = \frac{5-x^2}{3-x},\; h(x) = x-4$$
Г) $$f(x) = \sqrt{x^2+6},\; g(x) = \frac{8-x^2}{3-x},\; h(x) = 2$$
Ответы:
1) $$x \in [2;\; \frac{17}{7}) \cup (3;6)$$
2) $$x \in (1-\sqrt{3};\; 1+\sqrt{3}) \cup (3;+\infty)$$
3) $$x \in (-\infty;-4)\cup(-2;0)$$
4) $$a \in (-\infty;-3)$$
| А | Б | В | Г |
От автора сайта:
Решать это задание не вижу смысла. Вам тоже не советую тратить время. Там каждый раз составляется система вида $$\left\{\begin{matrix} f(x)>h(x)\\ g(x)>h(x) \end{matrix}\right.$$.
Не тяжело, но руками это набирать на сайт не буду.
Задание 10
Чтобы перевести значение температуры по шкале Цельсия в шкалу Фаренгейта, пользуются формулой $$t_F = 1,8t_C + 32$$, где $$t_C$$ — температура в градусах Цельсия, $$t_F$$ — температура в градусах Фаренгейта. Скольким градусам по шкале Фаренгейта соответствует $$-25$$ градусов по шкале Цельсия?
$$t_F = 1,8\cdot(-25) + 32=-13$$
Задание 11
Решите систему неравенств:
$$\left\{\begin{aligned} 4(9x + 3) - 9(4x + 3) > 3x \\ (x - 2)(x + 9) 0 \end{aligned}\right.$$
1) $$( -9;\ -5 )$$
2) $$( -5;\ 2 )$$
3) $$( -9;\ 2 )$$
4) $$( -\infty;\ -9 )$$
$$\left\{\begin{matrix} 4(9x+3)-9(4x+3)>3x\\ (x-2)(x+9)<0 \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} 36x+12-36x-27-3x>0\\ (x-2)(x+9)<0 \end{matrix}\right.\Leftrightarrow$$
$$\Leftrightarrow\left\{\begin{matrix} -3x>-15\\ x>-9\\ x<2 \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} x<-5\\ x>-9\\ x<2 \end{matrix}\right.\Leftrightarrow x\in(-9;-5)\Rightarrow 1$$
Задание 12
В ходе распада радиоактивного изотопа его масса уменьшается вдвое каждые $$9$$ минут. В начальный момент масса изотопа составляла $$320$$ мг. Найдите массу изотопа через $$63$$ минуты. Ответ дайте в миллиграммах.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Можно записать следующую зависимость оставшейся массы $$m$$ изотопа от времени $$t$$ мин, зная исходную массу $$M = 320$$ мг и период полураспада $$T = 9$$ мин:
$$m=\frac{M}{2^{\frac{t}{T}}}$$ мг.
Подставим в эту формулу время $$t=63$$ мин и вычислим массу $$m$$, получим:
$$m=\frac{320}{2^{\frac{63}{9}}}=\frac{320}{2^7}=\frac{320}{128}=2,5$$ мг.
Задание 13
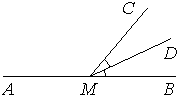
На прямой $$AB$$ взята точка $$M$$. Причём точка $$M$$ лежит между точками $$A$$ и $$B$$. Точка $$C$$ не лежит на прямой $$AB$$. Луч $$MD$$ — биссектриса угла $$CMB$$. Известно, что $$\angle DMC = 29^\circ$$. Найдите угол $$CMA$$. Ответ дайте в градусах.
Задание 14
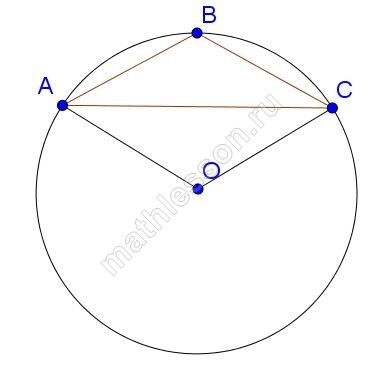
Боковая сторона равнобедренного треугольника равна $$5$$. Угол при вершине, противолежащий основанию, равен $$120^\circ$$. Найдите диаметр окружности, описанной около этого треугольника.
Пусть угол B равен 120 градусам, тогда $$\smile AC = 240^{\circ}$$ (по свойству вписанного угла), тогда меньшая дуга CA равна $$360-240=120^{\circ}$$, и центральный угол, опирающийся на эту дугу так же составляет 120 градусов ($$\angle AOC$$). Так как треугольники ABC и ACO равнобедренные, имею общую сторону и равные углы против этой стороны, то они между собой равны, следовательно, AO=5=r, где r - радиус окружности, следовательно, диаметр окружности равен 10
Задание 17
Какие из следующих утверждений верны? Если верных утверждений несколько, запишите их номера в порядке возрастания без пробелов, запятых и других разделительных символов.
- На плоскости существует единственная точка, равноудалённая от концов отрезка.
- В любой треугольник можно вписать окружность.
- Если в параллелограмме две смежные стороны равны, то такой параллелограмм является ромбом.
1) неверно, т. к. существует бесконечное множество таких точек, и все они располагаются на серединном перпендикуляре
2) верно, по свойству треугольника
3) верно, т. к. если две смежные стороны равны, то и все стороны в параллелограмме равны.
Задание 19
Моторная лодка прошла против течения реки $$72$$ км и вернулась в пункт отправления, затратив на обратный путь на $$2$$ часов меньше, чем на путь против течения. Найдите скорость (в км/ч) лодки в неподвижной воде, если скорость течения реки равна $$3$$ км/ч.
$$x$$ км/час - собственная скорость лодки
$$x+3$$ км/час - скорость лодки по течению
$$x-3$$ км/час - скорость лодки против течения
$$\frac{72}{x+3}$$ - время пути лодки по течению,
$$\frac{72}{x-3}$$ - время пути лодки против течения.
В задаче сказано, что на обратный путь (по течению) лодка затратила на 2 часа меньше, чем против течения. Отсюда равенство:
$$\frac{72}{x-3}-\frac{72}{x+3}=2$$
$$72(x+3)-72(x-3)=2(x+3)(x-3)$$
$$72x+216-72x+216=2x^2-18 \Leftrightarrow 2x^2=450 \Leftrightarrow x^2=225 \Rightarrow$$
$$\Rightarrow |x|=\sqrt{225} \Rightarrow x_1=15$$ и $$x_2=-15$$ - не подходит по смыслу задачи.
$$x=15$$ км/час
Задание 20
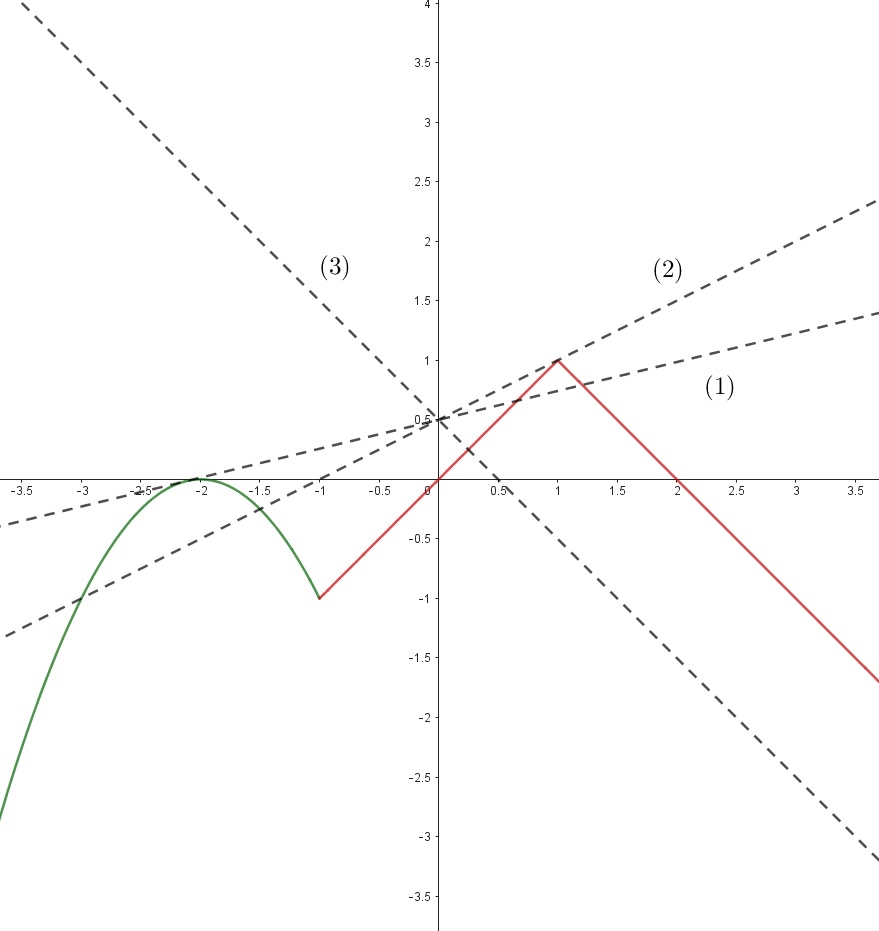
Постройте график функции $$y = \left\{\begin{aligned} -x^2 - 4x - 4, & x < -1 \\ 1 - |x - 1|, & x \geq -1 \end{aligned}\right.$$ Определите, при каких значениях $$a$$ прямая $$y = ax + \frac{1}{2}$$ имеет с графиком ровно две общие точки.
Учтём, что $$y=-x^2-4x-4=-(x+2)^2$$ - парабола, смещенная по Ox влево на 2 и перевернутая.
$$y=1-|x-1|$$ - график $$y=|x|$$, смещенный по Ox вправо на 1, по Oy вверх на 1 и перевернутый.
Найдём, когда $$y=ax+\frac{1}{2}$$ имеет с $$y=-(x+2)^2$$ одну общую точку (1).
$$ax+\frac{1}{2}=-x^2-4x-4$$
$$x^2+x(4+a)+4,5=0$$
$$D=(4+a)^2-4\cdot4,5=0$$
$$4+a=\pm\sqrt{18}\Rightarrow a=-4\pm3\sqrt{2}$$. При этом в случае (1) имеем $$a>0\Rightarrow a=3\sqrt{2}-4$$.
Найдём, когда проходит $$y=ax+\frac{1}{2}$$ через (1;1):
$$1=a+\frac{1}{2}\Rightarrow a=\frac{1}{2}$$
Учтём, что при $$a\leq-1$$ имеем 1 точку (3).
Тогда $$a\in(-1;3\sqrt{2}-4)\cup(\frac{1}{2};+\infty)$$