ОГЭ математика 2023. Разбор варианта Алекса Ларина № 330.
Больше разборов на моем ютуб-канале
Задание 1-5
Участок
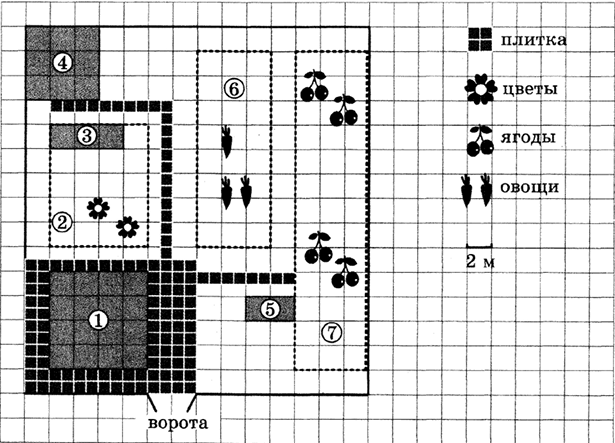
На плане (см. рис. выше) изображён дачный участок. Сторона каждой клетки на плане соответствует 2 м. Участок имеет прямоугольную форму. Въезд и выезд осуществляются через единственные ворота. При въезде на участок слева от ворот находится жилой дом. Помимо жилого дома, на участке есть баня площадью 36 м2. Между жилым домом и баней находится цветник с теплицей. Теплица отмечена на плане цифрой 3. Напротив жилого дома находится бак с водой для полива растений, за ним плодово‐ягодные кустарники. В глубине участка есть огород для выращивания овощей, отмеченный цифрой 6. Все дорожки внутри участка имеют ширину 1 м и застелены садовым покрытием, состоящим из плит размером 1 м × 1 м. Площадка вокруг дома выложена такими же плитами. К дачному участку подведено электричество. Имеется магистральное газоснабжение.
$$1.$$ Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу. В ответе запишите последовательность четырёх цифр без пробелов, запятых и других разделительных символов.
| Объекты | жилой дом | баня | бак | цветник |
|---|---|---|---|---|
| Цифры |
$$2.$$ Плиты для садовых дорожек продаются в упаковках по 4 штуки. Сколько упаковок плит понадобилось, чтобы выложить все дорожки и площадку вокруг дома?
$$3.$$ Найдите площадь (в м2) дома.
$$4.$$ Найдите расстояние от бака с водой до бани (расстояние между двумя ближайшими точками по прямой) в метрах.
$$5.$$ Хозяин участка планирует установить в жилом доме систему отопления. Он рассматривает два варианта: электрическое или газовое отопление. Цены на оборудование и стоимость его установки, данные о расходе газа, электроэнергии и их стоимости даны в таблице (см. ниже).
Обдумав оба варианта, хозяин решил установить газовое отопление. Через сколько часов непрерывной работы отопления экономия от использования газа вместо электричества компенсирует разницу в стоимости покупки и установки газового и электрического оборудования?
| Отопление | Газовое | Электрическое |
|---|---|---|
| Стоимость нагревателя (котла) (руб.) | 23 000 | 17 000 |
| Стоимость монтажа (руб.) | 17 784 | 13 000 |
| Средний расход газа (м3/ч) | 1,4 | - |
| Средняя потребляемая мощность (кВт) | - | 4,6 |
| Стоимость газа (руб./м3) | 4,5 | - |
| Стоимость электроэнергии (руб./(кВт∙ч)) | - | 4,3 |
$$9+13+8+8+16+44+22=120$$ - всего плиток
$$\frac{120}{4}=30$$ - упаковок
$$S=4\cdot4\cdot2\cdot2=64$$
$$n=\frac{23000-17000+17784-13000}{4,6\cdot4,3-4,5\cdot1,4}=\frac{6000+4784}{19,78-6,3}=\frac{10784}{13,48}=800$$
Задание 10
Дана функция $$f(x) = x^2 + 1$$. Установите соответствие между уравнениями и их решениями. В ответе запишите последовательность цифр, соответствующих A, Б, В, Г, без пробелов, запятых и других разделительных символов.
Уравнения
A) $$f(3t - 1) = f(1 - 2t)$$
Б) $$f(-3t^2 + 5t - 7) = f(-55 - 5t + 4t^2)$$
В) $$f(2t - 3) = f(\frac{1}{3}t - 5)$$
Г) $$f(3\sqrt{t} - 5) = f(39 - 10t)$$
Решения
1) $$\left\{0;\; \frac{5}{6}\right\}$$
2) $$\left\{-2;\; \frac{24}{7};\; \pm\sqrt{62}\right\}$$
3) $$\left\{\frac{7}{6};\; 2\right\}$$
4) $$\left\{4;\; \frac{889 - 3\sqrt{1769}}{200}\right\}$$
1) $$f(3t-1)=(3t-1)^2+1; f(1-2t)=(1-2t)^2+1.$$
$$f(3t-1)=f(1-2t)\Leftrightarrow (3t-1)^2+1=(1-2t)^2+1\Leftrightarrow$$
$$\Leftrightarrow\left[\begin{matrix} 3t-1=1-2t\\ 3t-1=-1+2t \end{matrix}\right.\Leftrightarrow\left[\begin{matrix} 5t=2\\ t=0 \end{matrix}\right.\Leftrightarrow\left[\begin{matrix} t=0,4\\ t=0 \end{matrix}\right.$$
$$f(3\cdot0-1)=f(-1)=(-1)^2+1=2$$
2) $$f(-3t^2+5t-7)=f(-55-5t+4t^2)\Rightarrow$$
$$\Rightarrow\left[\begin{matrix} -3t^2+5t-7=-55-5t+4t^2\\ -3t^2+5t-7=55+5t-4t^2 \end{matrix}\right.\Leftrightarrow\left[\begin{matrix} 7t^2-10t-48=0\\ t^2=62 \end{matrix}\right.\Leftrightarrow\left[\begin{matrix} t=-2;\frac{24}{7}\\ t=\pm\sqrt{62} \end{matrix}\right.$$
3) $$\left[\begin{matrix} 2t-3=\frac{1}{3t-5}\\ 2t-3=\frac{1}{5-3t} \end{matrix}\right.\Leftrightarrow\left[\begin{matrix} 6t^2-19t+15=1\\ -6t^2+19-15=1 \end{matrix}\right.\Leftrightarrow\left[\begin{matrix} 6t^2-19t+14=0\\ 6t^2-19t+16=0 \end{matrix}\right.\Leftrightarrow\left[\begin{matrix} t=2\\ t=\frac{7}{6} \end{matrix}\right.$$
Получим $$1;2;3;4.$$
Задание 11
Площадь ромба $$S$$ можно вычислить по формуле $$S = \frac{1}{2}d_1d_2$$, где $$d_1$$ и $$d_2$$ — диагонали ромба. Пользуясь этой формулой, найдите диагональ $$d_1$$, если диагональ $$d_2$$ равна $$30$$, а площадь ромба $$120$$.
Задание 12
Решите систему неравенств:
$$\left\{\begin{aligned} -9 + 3x > 0 \\ 2 - 3x > -10 \end{aligned}\right.$$
1) $$\varnothing$$
2) $$( 3;\ 4 )$$
3) $$( -\infty;\ 4 )$$
4) $$( 3;\ +\infty )$$
$$\left\{\begin{matrix} -9+3x>0\\ 2-3x>-10 \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} 3x>9\\ -3x>-12 \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} x>3\\ x<4 \end{matrix}\right.\Rightarrow 2.$$
Задание 13
Мама договорилась с Димой, что в понедельник он будет учить испанские слова. За первое выученное слово она даст сыну $$5$$ конфет, а за каждое следующее слово — на $$2$$ конфеты больше, чем за предыдущее. Сколько конфет Дима получит от мамы в понедельник, если он выучит $$12$$ слов?
Растущее количество конфет составляет арифметическую прогрессию $$5+7+9+...$$ с первым членом a1 = 5, разностью d = 2. Сумму первых 12 членов прогрессии $$S_n=\frac{2a_1+d(n-1)}{2}\cdot n:$$
$$S_{12}=\frac{2\cdot5+2(12-1)}{2}\cdot12=192$$ конфеты.
Задание 15
На окружности отмечены точки $$A$$ и $$B$$ так, что меньшая дуга $$AB$$ равна $$66^\circ$$. Прямая $$BC$$ касается окружности в точке $$B$$ так, что угол $$ABC$$ острый. Найдите угол $$ABC$$. Ответ дайте в градусах.
$$\angle ABC$$ - угол между хордой и касательной. Он равен половине величины отсекаемой дуги, то есть $$33^{\circ}.$$
Задание 16
На клетчатой бумаге изображена трапеция $$ABCD$$. Найдите длину её средней линии, если известно, что $$AD = 3\sqrt{2}$$.
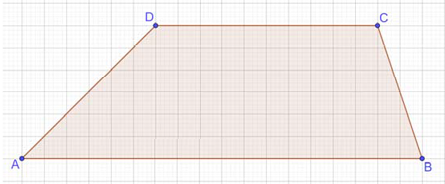
Пусть $$DH$$ - высота. Тогда $$DH = 6$$ клеток, $$AH = 6$$ клеток.
$$(6x)^2+(6x)^2=(3\sqrt{2})^2\Leftrightarrow 72x^2=18\Rightarrow x^2=\frac{1}{4}\Rightarrow x=0,5$$
Средняя линия равна $$\frac{10+18}{2}=14$$ клеток $$\Rightarrow 14\cdot0,5=7$$
Задание 17
Дан правильный шестиугольник $$ABCDEF$$ и равные друг другу шесть правильных треугольников $$GID$$, $$JIG$$, $$HIJ$$, $$HGL$$, $$MHL$$, $$AHM$$ (см. рисунок). Найдите сумму площадей этих шести треугольников, если известно, что площадь шестиугольника $$ABCDEF$$ равна $$90$$.
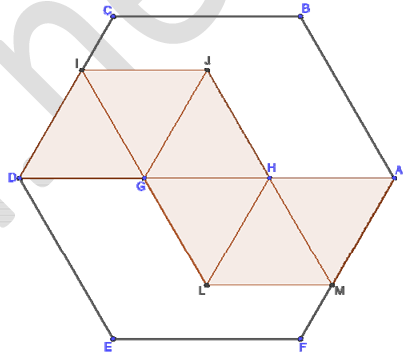
Пусть $$O$$ - центр $$GH.$$ Тогда $$OH$$ - сторона шестиугольника. Он состоит из 6 равносторонних треугольников со стороной равной $$GH.$$ Пусть $$GH=a.$$
Тогда $$S_{ABCDEF}=6\cdot\frac{1}{2}\cdot a\cdot a\cdot\frac{\sqrt{3}}{2}=\frac{3a^2\sqrt{3}}{2}=90\Rightarrow a^2\sqrt{3}=60.$$
При этом $$DG=\frac{DA}{3}=\frac{a\cdot2}{3}.$$
$$D_{DGI}=\frac{1}{2}\cdot\frac{2a}{3}\cdot\frac{2a}{3}\cdot\frac{\sqrt{3}}{2}=\frac{a^2\sqrt{3}}{9}.$$
Тогда 6 таких треугольников $$6\cdot\frac{a^2\sqrt{3}}{9}=\frac{2a^2\sqrt{3}}{3}=\frac{2\cdot60}{3}=40.$$
Задание 18
Какие из следующих утверждений верны? Если верных утверждений несколько, запишите их номера в порядке возрастания без пробелов, запятых и других разделительных символов.
- В треугольнике против меньшего угла лежит меньшая сторона.
- В треугольнике против меньшей стороны лежит больший угол.
- В треугольнике против меньшей стороны лежит меньший угол.
- В треугольнике $$ABC$$, в котором внутренние углы $$\angle A = 40^{\circ}$$, $$\angle B = 60^{\circ}$$, сторона $$AC$$ наибольшая.
1) верно
2) нет, против меньшей стороны меньший угол
3) верно
4) $$\angle C=180^{\circ}-(40^{\circ}+60^{\circ})=80^{\circ}$$ - больший угол, тогда большая сторона $$AB\Rightarrow$$ нет
Задание 20
Из пункта $$A$$ в пункт $$B$$, расположенный ниже по течению реки, отправился плот. Одновременно навстречу ему из пункта $$B$$ вышел катер. Встретив плот, катер сразу повернул и поплыл назад. Какую часть пути от $$A$$ до $$B$$ пройдет плот к моменту возвращения катера в пункт $$B$$, если скорость катера в стоячей воде вчетверо больше скорости течения реки?
Пусть скорость течения реки х км/ч, следовательно, у плота тоже скорость х км/ч.
Из этого следует, что скорость катера по течению $$4x + x = 5x$$ км/ч, а против течения – $$4x – x = 3х$$ км/ч. Скорость сближения катера и плота $$3x + x = 4x$$ км/ч.
Встретились они через $$\frac{AB}{4x}$$ ч. За это время плот пройдет расстояние, равное:
$$x\cdot\frac{AB}{4x}=\frac{AB}{4},$$ а катер – $$\frac{3\cdot AB}{4}.$$
А на обратный путь катер потратит $$\frac{\frac{3AB}{4}}{5x}=\frac{3AB}{20x} $$ч.
За это время плот проплывет расстояние:
$$x\cdot\frac{3AB}{20x}=\frac{3AB}{20},$$ а всего он проплывет $$\frac{AB}{4}+\frac{3AB}{20}=\frac{2AB}{5},$$ то есть $$\frac{2}{5}=0,4$$ пути.
Задание 21
Первая прямая проходит через точки $$\left(0;\,\frac{9}{2}\right)$$ и $$(3;\,6)$$. Вторая прямая проходит через точки $$(1;\,2)$$ и $$(-4;\,7)$$. Найдите координаты общей точки этих двух прямых.
Уравнение первой прямой
$$\frac{x}{3}=\frac{y-4,5}{1,5}$$
$$1,5x-3y+13,5=0 $$
Уравнение второй прямой
$$\frac{x-1}{-5}=\frac{y-2}{5}$$
$$5x+5y-15=0$$
$$\left\{\begin{matrix} 3y-1,5x=13,5\\ x+y=3 \end{matrix}\right.$$
$$x=3-y$$
$$3y-1,5(3-y)=13,5$$
$$3y-4,5+1,5y=13,5$$
$$4,5y=18$$
$$y=4$$
$$x=-1$$
$$(-1;4)$$
Задание 22
Диагонали $$AC$$ и $$BD$$ трапеции $$ABCD$$ пересекаются в точке $$O$$. Площади треугольников $$AOD$$ и $$BOC$$ равны соответственно $$25$$ и $$16$$. Найдите площадь трапеции.
Треугольники AOD и COB подобны.
Далее, очень легко построить треугольник, подобный этим треугольникам, площадь которого равна площади трапеции.
Из точки C проводится прямая CE II BD до пересечения с продолжением AD в точке E.
Треугольник ACE имеет ту же высоту, что и трапеция (собственно, у них общая высота - расстояние от точки C до AD).
Поскольку DBCE - параллелограмм, то $$AE = AD + DE = AD + BC$$
То есть площадь треугольника ACE равна площади S трапеции ABCD;
Треугольник ACE подобен AOD и COB по построению (у них, к примеру, равны все углы).
Площади подобных треугольников пропорциональны квадратам соответственных сторон.
То есть СУЩЕСТВУЕТ такое число k, что
$$AD=k\cdot\sqrt{25};$$ $$BC=k\cdot\sqrt{16};$$ $$AD+BC=k\cdot\sqrt{S};$$
Отсюда:
$$\sqrt{S}=\sqrt{25}+\sqrt{16}=9$$
$$S=81$$
Задание 23
Через точку $$O$$ пересечения диагоналей параллелограмма $$ABCD$$ проведена прямая, пересекающая стороны $$AB$$ и $$CD$$ в точках $$E$$ и $$F$$ соответственно. Докажите, что отрезки $$AE=CF$$.
Треугольники AOE и COF равны по стороне и двум прилежащим к ней углам: AO = CO, поскольку диагонали параллелограмма точкой пересечения делятся пополам, $$\angle AOE=\angle COF$$ как вертикальные, $$\angle OAE=\angle OCF$$ как накрест лежащие углы при пересечении параллельных прямых AB и CD секущей AC. Из равенства треугольников следует равенство их сходственных сторон: AE = CF. Что и требовалось доказать.
Задание 24
В треугольнике $$ABC$$ биссектриса угла $$A$$ делит высоту, проведённую из вершины $$B$$, в отношении $$5:4$$, считая от точки $$B$$. Найдите радиус окружности, описанной около треугольника $$ABC$$, если $$BC=12$$.
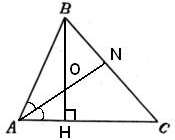
По условию задачи BO:OH=5:4, следовательно, OH:BO=4:5. По свойству биссектрисы AH:AB=HO:BO=4:5, но AH:AB – это косинус угла A, то есть $$\cos\angle A=\frac{4}{5}.$$ Рассмотрим прямоугольный треугольник AHB, в котором условно катет AH=4, а гипотенуза AB=5. По теореме Пифагора находим
$$BH=\sqrt{25-16}=3$$.
Тогда синус угла A равен $$\sin\angle A=\frac{3}{5}.$$ По следствию теоремы синусов имеем:
$$\frac{BC}{\sin A}=2R,$$
где R – радиус описанной окружности. Следовательно,
$$R=\frac{BC}{2\sin A}=\frac{12}{2\cdot0,6}=10.$$