ОГЭ математика 2023. Разбор варианта Алекса Ларина № 336.
Больше разборов на моем ютуб-канале
Задание 1-5
Листы
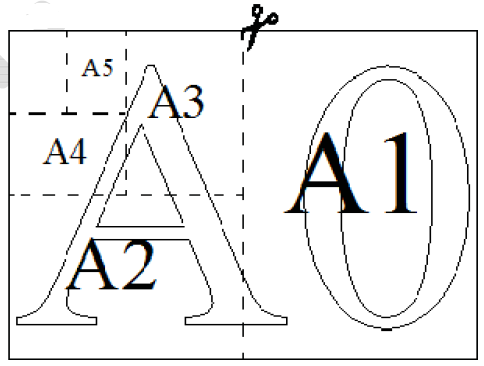
Общепринятые форматы листов бумаги обозначают буквой А и цифрой: А0, А1, А2 и так далее. Лист формата А0 имеет форму прямоугольника, площадь которого равна 1 кв. м. Если лист формата А0 разрезать пополам параллельно меньшей стороне, получается два равных листа формата А1. Если лист А1 разрезать так же пополам, получается два листа формата А2. И так далее. Отношение большей стороны к меньшей стороне листа каждого формата одно и то же, поэтому листы всех форматов подобны. Это сделано специально для того, чтобы пропорции текста и его расположение на листе сохранялись при уменьшении или увеличении шрифта при изменении формата листа. 1. В таблице даны размеры (с точностью до мм) четырёх листов, имеющих форматы А0, А1, А3 и А4.| Номер листа | Длина (мм) | Ширина (мм) |
|---|---|---|
| 1 | 297 | 210 |
| 2 | 420 | 297 |
| 3 | 1189 | 841 |
| 4 | 841 | 594 |
| Формат | A0 | A1 | A3 | A4 |
|---|---|---|---|---|
| Номер |
Задание 7
Сравните числа $$a$$ и $$b$$, если $$a = (7,3 \cdot 10^{-4}) \cdot (2 \cdot 10^{-4})$$ и $$b = 0,00000015$$.
1) $$a b$$
2) $$a = b$$
3) $$a > b$$
В ответе запишите номер правильного варианта ответа.
$$0,00000015=15\cdot10^{-8}$$
$$(7,3\cdot10^{-4})\cdot(2\cdot10^{-4})=14,6\cdot10^{-8}$$
$$\Rightarrow b>a\Rightarrow 1.$$
Задание 10
Найдите все такие значения $$x$$, при каждом из которых график функции $$y = f(x)$$ лежит ниже графика функции $$y = g(x)$$. Установите соответствие между функциями и найденными значениями $$x$$. В ответе запишите последовательность цифр, соответствующих А, Б, В, Г, без пробелов, запятых и других разделительных символов.
Функции:
A) $$f(x) = 1 - \frac{4}{x-2},\; g(x) = \frac{5}{x^2-4x+4}$$
Б) $$f(x) = 1 - \frac{4}{x-3},\; g(x) = \frac{5}{x^2-6x+9}$$
В) $$f(x) = \frac{5x-2}{4x+3},\; g(x) = \frac{6x-4}{5x+1}$$
Г) $$f(x) = x^2 + 3x - 4,\; g(x) = -x^2 + 5x + 8$$
Ответы:
1) $$\left(-\frac{3}{4};-\frac{1}{5}\right) \cup (2;5)$$
2) $$(2;3)\cup(3;8)$$
3) $$(1;2)\cup(2;7)$$
4) $$(-2;3)$$
| А | Б | В | Г |
А)
$$1-\frac{4}{x-2}<\frac{5}{x^2-4x+4}\Leftrightarrow1-\frac{4}{x-2}<\frac{5}{(x+2)^2}\Rightarrow$$
$$\Rightarrow\left\{\begin{matrix} (x-2)^2-4(x-x)-5<0\\ x\neq2 \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} x^2-8x+7<0\\ x\neq2 \end{matrix}\right.\Leftrightarrow$$
$$\Leftrightarrow\left\{\begin{matrix} (x-7)(x-1)<0\\ x\neq2 \end{matrix}\right.\Rightarrow 3$$
Б)
$$1-\frac{4}{x-3}<\frac{5}{x^2-6x+9}\Rightarrow\left\{\begin{matrix} (x-3)^2-4(x-3)-5<0\\ x\neq3 \end{matrix}\right.\Leftrightarrow$$
$$\Leftrightarrow\left\{\begin{matrix} x^2-10x+16<0\\ x\neq3 \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} (x-2)(x-8)<0\\ x\neq3 \end{matrix}\right.\Rightarrow 2$$
Г)
$$x^2+3x-4<-x^2+5x+8\Rightarrow 2x^2-2x-12<0\Rightarrow x^2-x-6<0\Rightarrow$$
$$\Rightarrow (x-3)(x+2)<0\Rightarrow 4$$
Получим $$3214$$.
Задание 11
Площадь трапеции $$S$$ можно вычислить по формуле $$S = \frac{1}{2}(a + b)h$$, где $$a$$, $$b$$ — основания трапеции, $$h$$ — высота. Пользуясь этой формулой, найдите высоту $$h$$, если основания трапеции равны $$5$$ и $$7$$, а её площадь $$24$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


$$h=\frac{2S}{a+b}=\frac{2\cdot24}{5+7}=4$$
Задание 12
Решите неравенство: $$3 - x \ge 3x + 5$$
1) $$( -\infty,\ -2 ]$$
2) $$[ -2,\ +\infty )$$
3) $$( -\infty,\ -\frac{1}{2} ]$$
4) $$[ -\frac{1}{2};\ +\infty )$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


$$3 - x\geq 3x + 5$$
$$-x-3x\geq5-3$$
$$-4x\geq2$$
$$x\leq-0,5\Rightarrow 3$$
Задание 13
В амфитеатре $$12$$ рядов. В первом ряду $$20$$ мест, а в каждом следующем на $$2$$ места больше, чем в предыдущем. Сколько всего мест в амфитеатре?
Воспользуемся формулой арифметической прогрессии.
$$a_1=20$$ мест, $$d = 2$$ места.
$$S_n=\frac{2a_1+d(n-1)}{2}n=\frac{2\cdot20+2(12-1)}{2}\cdot12=372$$
Задание 15
Найдите величину (в градусах) вписанного в окружность угла, опирающегося на хорду, равную радиусу окружности. В ответе запишите произведение найденных значений.
Задание 16
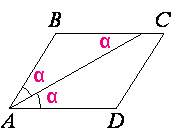
Найдите меньший угол (в градусах) равнобедренной трапеции $$ABCD$$, если диагональ $$AC$$ образует с основанием $$BC$$ и боковой стороной $$CD$$ углы, равные $$30^\circ$$ и $$105^\circ$$ соответственно.
$$30^{\circ}+105^{\circ}=135^{\circ}$$
$$180^{\circ}-135^{\circ}=45^{\circ}$$
$$45^{\circ}<135^{\circ}$$
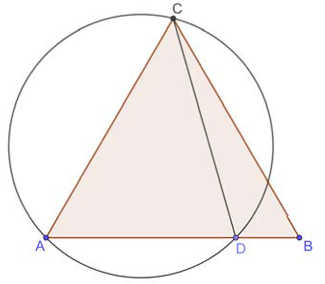
Задание 17
$$S=\pi R^2=27\pi\Rightarrow R=\sqrt{27}=3\sqrt{3}$$ - радиус описанной окружности около $$\Delta ACD$$
$$\frac{CD}{2\sin A}=R\Rightarrow CD=R\cdot2\sin A=3\sqrt{3}\cdot2\cdot\frac{\sqrt{3}}{2}=9$$
Задание 18
Какие из следующих утверждений верны? Если верных утверждений несколько, запишите их номера в порядке возрастания без пробелов, запятых и других разделительных символов.
- Если при пересечении двух прямых третьей прямой соответственные углы равны $$37^{\circ}$$, то эти две прямые параллельны.
- Через любые три точки проходит не более одной прямой.
- Сумма вертикальных углов равна $$180^{\circ}$$.
1) верно, соответственные углы при двух параллельных прямых равны.
2) верно. Если начертить 3 точки произвольно, прямую провести через них не удастся, но если они будут на одной линии, то по ним можно будет провести только одну прямую.
3) неверно, вертикальные углы образуются из 2-х пересекающихся прямых, одна сторона одного угла является продолжением стороны другого угла. Вертикальные углы равны, но не всегда в сумме дают 180°.
Задание 19
Решите уравнение $$ \frac{x}{x - 4} - \frac{1}{x + 1} = \frac{2 - x}{x + 1} + \frac{3}{x - 4} $$
$$\frac{x}{x-4}-\frac{1}{x+1}=\frac{2-x}{x+1}+\frac{3}{x-4}\Leftrightarrow\frac{x}{x-4}-\frac{3}{x-4}=\frac{2-x}{x+1}+\frac{1}{x+1}\Leftrightarrow$$
$$\Leftrightarrow\frac{x-3}{x-4}=\frac{3-x}{x+1}\Leftrightarrow\frac{x-3}{x-4}-\frac{3-x}{x+1}=0\Rightarrow\frac{x-3}{x-4}+\frac{x-3}{x+1}=0\Rightarrow$$
$$\Rightarrow (x-3)(\frac{1}{x-4}+\frac{1}{x+1})=0\Rightarrow\left[\begin{matrix} x-3=0\\ \frac{x+1+x-4}{x-4}=0 \end{matrix}\right.\Rightarrow\left[\begin{matrix} x=3\\ 2x-3=0 \end{matrix}\right.\Leftrightarrow\left[\begin{matrix} x=3\\ x=1,5 \end{matrix}\right.$$
Задание 20
Чтобы накачать в бак $$117$$ л воды, требуется на $$5$$ минут больше времени, чем на то, чтобы выкачать из него $$96$$ л воды. За одну минуту можно выкачать на $$3$$ л воды больше, чем накачать. Сколько литров воды накачивается в бак за минуту?
Пусть $$x$$ л/мин накачивает, тогда $$x+3$$ л/мин выкачивает. Время накачки $$t_{1}=\frac{117}{x}$$; время выкачивания $$t_{2}=\frac{96}{x+3}$$. При этом накачивает на 5 часов дольше, то есть: $$t_{1}-t_{2}=5$$, тогда:
$$\frac{117}{x}-\frac{96}{x+3}=5\quad |\cdot x(x+3)\Leftrightarrow 117x+351-96x=5x^{2}+15x\Leftrightarrow$$
$$\Leftrightarrow5x^{2}-6x-351=0\Rightarrow D=36+7020=7056=84^{2}\Rightarrow x_{1}=\frac{6+84}{10}=9, x_{2}<0$$, то есть накачивает по 9 л/мин.
Задание 21
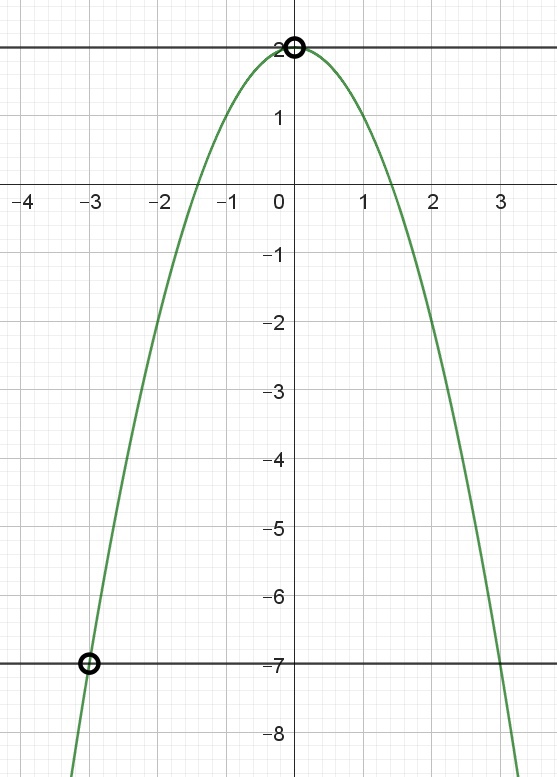
Постройте график функции $$y = 2 - \frac{x^4 + 3x^3}{x^2 + 3x}$$. Определите, при каких значениях $$a$$ прямая $$y = a$$ имеет с графиком этой функции ровно две общие точки.
Задание 22
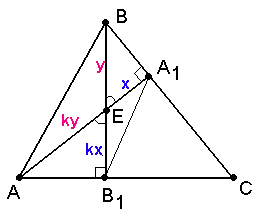
Высоты $$AA_{1}$$ и $$BB_{1}$$ остроугольного треугольника $$ABC$$ пересекаются в точке $$E$$. Докажите, что углы $$AA_{1}B_{1}$$ и $$ABB_{1}$$равны.
Задание 23
Боковые стороны $$AB$$ и $$CD$$ трапеции $$ABCD$$ равны соответственно $$24$$ и $$26$$, а основание $$BC$$ равно $$8$$. Биссектриса угла $$ADC$$ проходит через середину стороны $$AB$$. Найдите площадь трапеции.
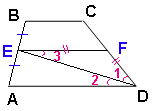 BC = 8
BC = 8AB = 24
CD = 26 EF средняя линия. ∆EFD равнобедренный (∠1=∠2 по условию, ∠3=∠2 как накрест лежащие ⇒ ∠1=∠3)
EF = FD = CD/2 = 26 / 2 = 13 AD = 2 EF - BC = 26 - 8 18 Предположим, что AB ⊥ AD
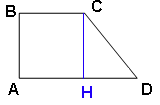 CH² = 26² - (18 - 8)² = 676 - 100 576 = AB² ⇒ CH = AB
Предположение верно ⇒ Высота трапеции h = AB
$$S = \frac{AD + BC)}{2}\cdot h=\frac{18+8}{2}\cdot24=312$$
CH² = 26² - (18 - 8)² = 676 - 100 576 = AB² ⇒ CH = AB
Предположение верно ⇒ Высота трапеции h = AB
$$S = \frac{AD + BC)}{2}\cdot h=\frac{18+8}{2}\cdot24=312$$