ОГЭ математика 2022. Разбор варианта Алекса Ларина № 292.
Больше разборов на моем ютуб-канале
Задание 1-5
Найдите значение выражения: $$\frac{(\frac{1}{6}-\frac{1}{2})\cdot \frac{-2-2,5}{2-2,5}\cdot (1,4^{2}-1,4)}{0,6}$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 6
Найдите значение выражения $$\frac{(a - 2b)^2 - 4b^2}{a}$$ при $$a = 0,3$$ и $$b = -0,35$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 7
Для экзамена подготовили билеты с номерами от $$1$$ до $$50$$. Какова вероятность того, что наугад взятый учеником билет имеет однозначный номер?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 8
На рисунке изображены графики трёх функций. Установите соответствие между этими графиками и формулами, которые их задают. В ответе укажите последовательность цифр, соответствующих А, Б, В, без пробелов и других разделительных символов между ними.
ГРАФИКИ
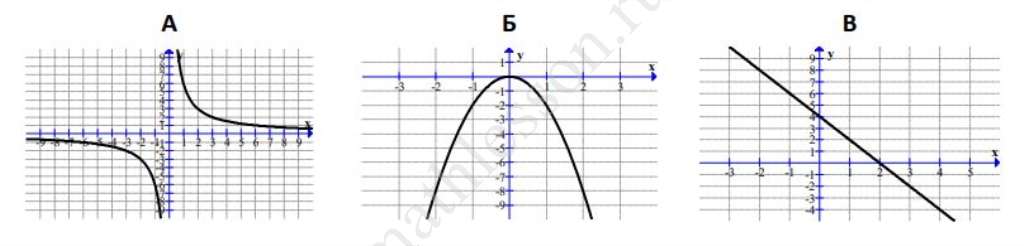
ФОРМУЛЫ
1. $$y = \frac{6}{x}$$
2. $$y = -2x + 4$$
3. $$y = -2x^2$$
В таблице под каждой буквой укажите соответствующий номер.
| А | Б | В |
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 9
Центростремительное ускорение при движении по окружности (в м/с²) можно вычислить по формуле $$a = \omega^2 R$$, где $$\omega$$ — угловая скорость (в с⁻¹), а $$R$$ — радиус окружности. Пользуясь этой формулой, найдите расстояние $$R$$ (в метрах), если угловая скорость равна $$0,5$$ с⁻¹, а центростремительное ускорение равно $$1,5$$ м/с².
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 10
При каких значениях $$a$$ выражение $$9a + 4$$ принимает положительные значения? В ответе укажите номер правильного варианта ответа.
1. $$a > -\frac{9}{4}$$
2. $$a -\frac{4}{9}$$
3. $$a -\frac{9}{4}$$
4. $$a >-\frac{4}{9}$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 11
В результате трёхкратного повышения цены на некоторый товар на одно и то же число процентов цена товара стала превышать первоначальную цену на $$72,8\%$$. На сколько процентов повышалась цена на товар каждый раз?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 12
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 13
Прямоугольный треугольник с катетами $$5$$ см и $$12$$ см вписан в окружность. Чему равен радиус (в см) этой окружности?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 14
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 16
Какие из следующих утверждений неверны? Если неверных утверждений несколько, запишите их номера в порядке возрастания без пробелов, запятых и других символов между ними.
- При пересечении двух параллельных прямых третьей прямой сумма накрест лежащих углов равна $$180^{\circ}$$.
- Диагонали ромба перпендикулярны.
- Центром окружности, описанной около треугольника, является точка пересечения его биссектрис.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 17
Рыболов в $$5$$ часов утра на моторной лодке отправился от пристани против течения реки, через некоторое время бросил якорь, $$2$$ часа ловил рыбу и вернулся обратно в $$10$$ часов утра того же дня. На какое расстояние (в км) от пристани он отплыл, если скорость реки равна $$2$$ км/ч, а собственная скорость лодки $$6$$ км/ч?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 18
Постройте график функции $$y = |x + 1| - |x - 1| - x$$ и найдите все значения $$k$$, при каждом из которых прямая $$y = kx$$ имеет с графиком данной функции ровно одну общую точку.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


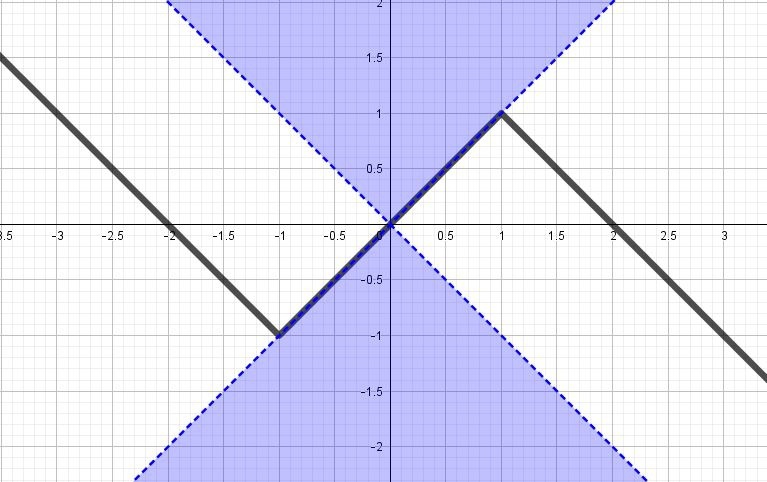
$$y=|x+1|-|x-1|-x$$
$$y=\left\{\begin{matrix} -x-1-(-x+1)-x,x\leq-1\\ x+1-(-x+1)-x,x\in(-1;1]\\ x+1-(x-1)-x,x>1 \end{matrix}\right.\Leftrightarrow y=\left\{\begin{matrix} -x-2,x\leq-1\\ x,x\in(-1;1]\\ -x+2,x>1 \end{matrix}\right.\Leftrightarrow$$
Ровно одну будет иметь при $$k>1$$ и $$k\in(-\infty;-1],$$ т.е. $$k\in (-\infty;-1]\cup(1;+\infty)$$
(на рисунке выделим зоны, где должен располагаться $$y=kx$$)
Задание 19
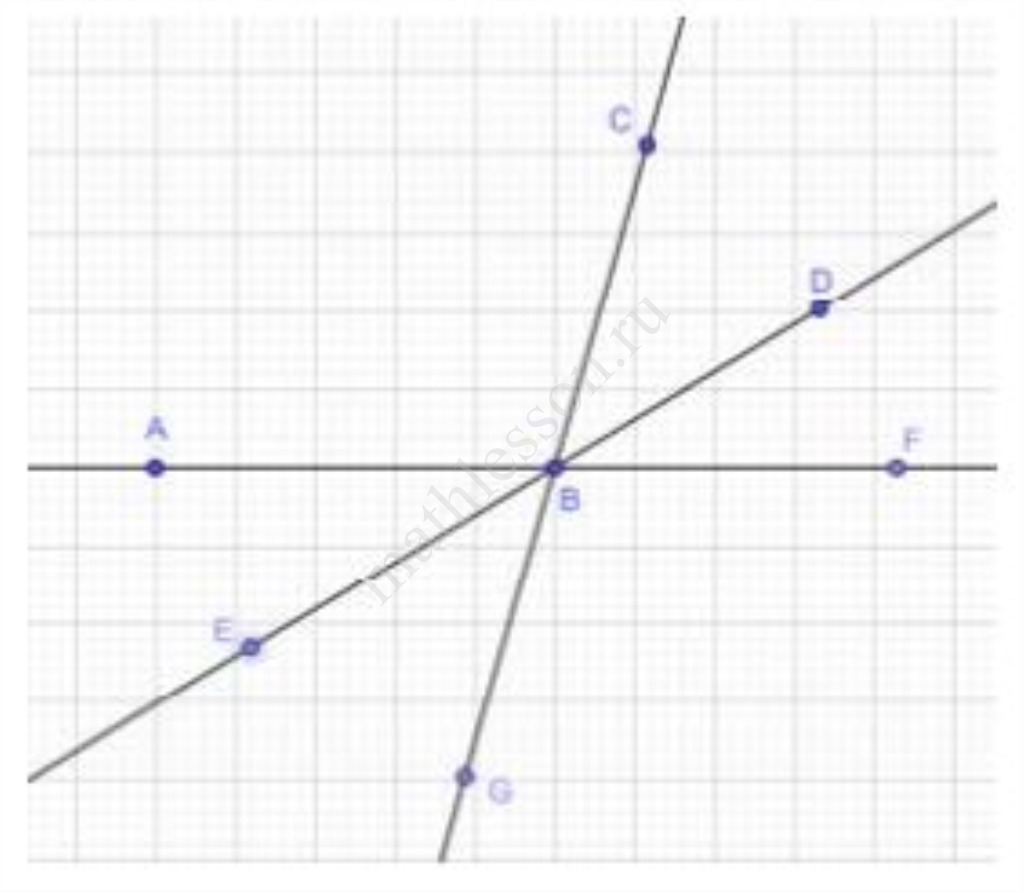
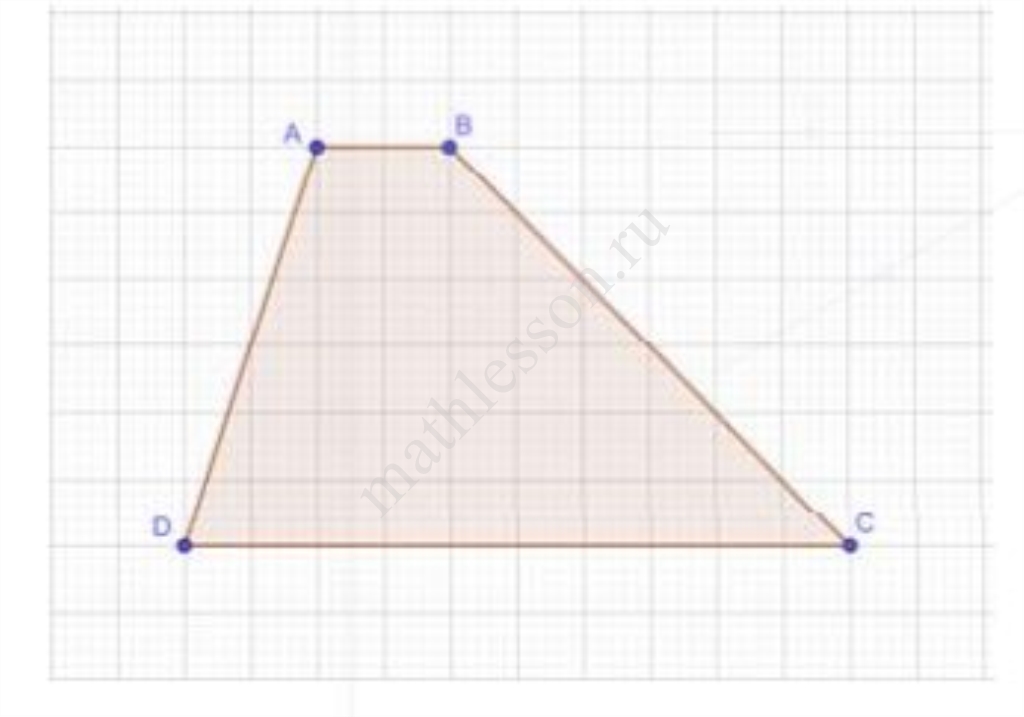
Биссектрисы углов $$C$$ и $$D$$ трапеции $$ABCD$$ пересекаются в точке $$P$$, лежащей на стороне $$AB$$. Докажите, что точка $$P$$ равноудалена от прямых $$BC$$, $$CD$$ и $$AD$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 20
Окружность радиуса $$4$$ касается внешним образом второй окружности в точке $$B$$. Общая касательная к этим окружностям, проходящая через точку $$B$$ пересекает некоторой другой их общей касательной в точке $$A$$. Найдите радиус второй окружности, если $$AB=6$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!