Задание 834
Задание 834
Радиус окружности с центром в точке $$O$$ равен $$50$$, длина хорды $$AB$$ равна $$96$$. Найдите расстояние от хорды $$AB$$ до параллельной ей касательной $$k$$. В ответе запишите произведение найденных значений.
Ответ: 2304
Скрыть
$$OA=50;OM\perp AB;OB=50\Rightarrow AM=MB=48\Rightarrow OM=\sqrt{50^2-48^2}=14$$
$$\Rightarrow MN=50-14=36$$
$$LM=50+14=64$$
$$LM\cdot MN=2304$$
Можно по свойству хорд: $$LM\cdot MN=AM\cdot MB=48\cdot48=2304$$
Аналоги к этому заданию:
Задание 4567
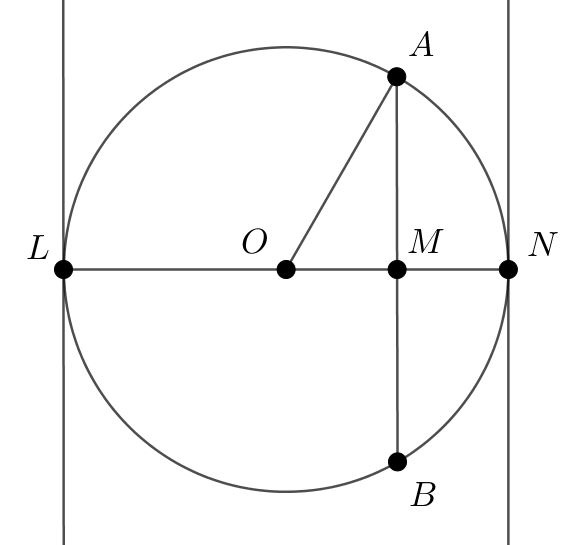
Радиус окружности с центром в точке $$O$$ равен $$85$$, длина хорды $$AB$$ равна $$80$$ (см. рисунок). Найдите расстояние от хорды $$AB$$ до параллельной ей касательной $$k$$.
Ответ: 160
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Скрыть
| $$OA=OM=85$$ $$AB=80$$ $$\Rightarrow AL=BL=40$$ $$OL=\sqrt{OA^{2}-AC^{2}}=\sqrt{85^{2}-40^{2}}=75$$ $$ML=MO+OL=85+75=160$$ |