Задание 831
Задание 831
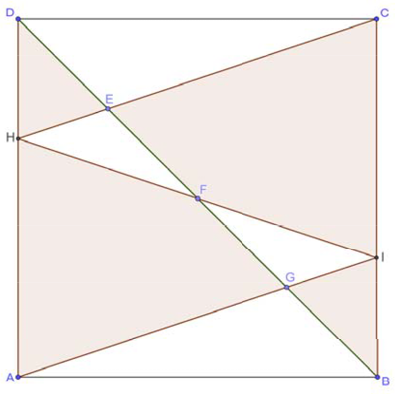
Дан квадрат $$ABCD$$. На его диагонали $$DB$$ отмечены точки $$E$$, $$F$$, $$G$$ таким образом, что $$DE = EF = FG = GB$$ (см. рисунок). Пусть $$H$$ — точка пересечения прямых $$AD$$ и $$CE$$, а $$I$$ — точка пересечения прямых $$HF$$ и $$BC$$. Найдите сумму площадей треугольников $$ABG$$, $$FGI$$, $$HFE$$ и $$DEC$$, если известно, что $$AC = 12\sqrt{2}$$.
Пусть $$S_{ABCD}=S.$$ Тогда:
$$S_{ADB}=\frac{S}{2};S_{AGB}=\frac{GB}{DB}S_{ADB}=\frac{1}{4}\cdot\frac{S}{2}=\frac{S}{8};\frac{HD}{CB}=\frac{DE}{EB}=\frac{1}{3}\Rightarrow AH=\frac{2}{3}AD$$
$$S_{AHI}=\frac{2}{3}\cdot\frac{1}{2}\cdot S=\frac{1}{3}S.$$ Тогда $$S_{FGI}=\frac{1}{2}\cdot\frac{1}{4}\cdot S_{AHI}=\frac{1}{8}\cdot\frac{1}{3}S=\frac{1}{24}S$$
Итого сумма: $$(\frac{S}{8}+\frac{S}{24})\cdot2=\frac{4S}{12}=\frac{4\cdot12^2}{12}=48$$
$$AB^2+AD^2=(12\sqrt{2})^2\Rightarrow AB^2=12^2=S$$
Аналоги к этому заданию:
Задание 852
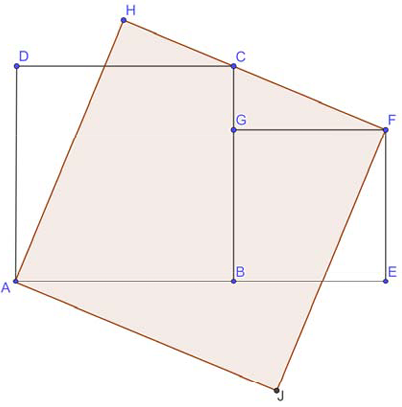
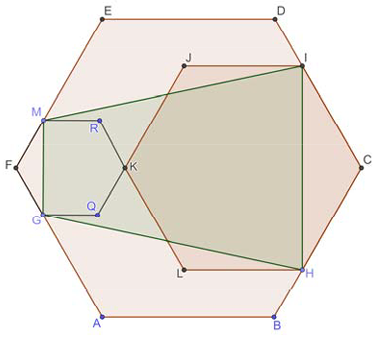
Дан правильный шестиугольник $$ABCDEF$$ и равные друг другу шесть правильных треугольников $$GID$$, $$JIG$$, $$HIJ$$, $$HGL$$, $$MHL$$, $$AHM$$ (см. рисунок). Найдите сумму площадей этих шести треугольников, если известно, что площадь шестиугольника $$ABCDEF$$ равна $$90$$.
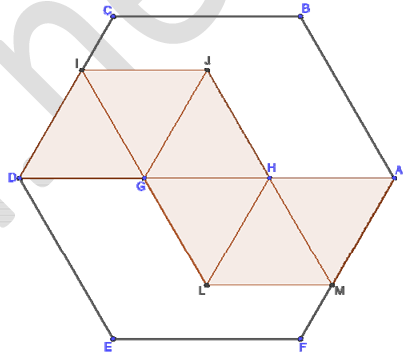
Пусть $$O$$ - центр $$GH.$$ Тогда $$OH$$ - сторона шестиугольника. Он состоит из 6 равносторонних треугольников со стороной равной $$GH.$$ Пусть $$GH=a.$$
Тогда $$S_{ABCDEF}=6\cdot\frac{1}{2}\cdot a\cdot a\cdot\frac{\sqrt{3}}{2}=\frac{3a^2\sqrt{3}}{2}=90\Rightarrow a^2\sqrt{3}=60.$$
При этом $$DG=\frac{DA}{3}=\frac{a\cdot2}{3}.$$
$$D_{DGI}=\frac{1}{2}\cdot\frac{2a}{3}\cdot\frac{2a}{3}\cdot\frac{\sqrt{3}}{2}=\frac{a^2\sqrt{3}}{9}.$$
Тогда 6 таких треугольников $$6\cdot\frac{a^2\sqrt{3}}{9}=\frac{2a^2\sqrt{3}}{3}=\frac{2\cdot60}{3}=40.$$
Задание 625
Даны три правильных шестиугольника $$ABCDEF$$, $$HCIJKL$$ и $$FGQKRM$$ (см. рисунок). Найдите площадь четырёхугольника $$IMGH$$, если известно, что $$AB = \frac{2\sqrt{2}}{\sqrt[4]{3}}$$.
Учтём, что $$FC=FK+KC\Rightarrow MR+JI=ED$$.
Получим: $$GM=MR\cdot\sqrt{3};\; IH=JI\cdot\sqrt{3}$$.
Пусть $$FC\cap MG=X;\; FC\cap IH=Y$$. Тогда $$XK=1,5MR;\; KY=1,5IJ$$.
Тогда $$S_{IMGH}=\frac{MG+IH}{2}\cdot XY=\frac{MR\cdot\sqrt{3}+JI\cdot\sqrt{3}}{2}(1,5MR+1,5IJ)=$$
$$=\frac{\sqrt{3}(MR+JI)}{2}\cdot1,5(MR+JI)=\frac{3\sqrt{3}}{4}ED^2=\frac{3\sqrt{3}}{4}\cdot(\frac{2\sqrt{2}}{\sqrt[4]{3}})^2=\frac{3\sqrt{3}}{4}\cdot\frac{4\cdot2}{\sqrt{3}}=6$$