Задание 799
Задание 799
Радиус $$OB$$ окружности с центром в точке $$O$$ пересекает хорду $$MN$$ этой окружности в её середине — точке $$K$$. Найдите длину хорды $$MN$$, если $$KB = 1$$, а радиус окружности равен $$13$$.
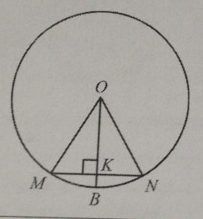
Построим радиусы ОН и ОМ.
Так как радиус ОВ перпендикулярен хорде МН, то треугольники ОКМ и ОКН прямоугольные.
В треугольниках ОКМ и ОКН катет ОК общий, а гипотенузы $$ОМ = ОН = R = 13$$ см.
Тогда прямоугольные треугольники ОКМ и ОКН равны по катету и гипотенузе, а значит $$КМ = КН.$$
Радиус $$ОВ = 13 = ВК + ОК = 1 + ОК.$$
$$ОК = 13 – 1 = 12$$ см.
По теореме Пифагора, из прямоугольного треугольника ОКН определим длину катета КН.
$$КН^2=ОН^2-ОК^2=169-144=25.$$
$$КН=5$$ см.
Тогда хорда $$МН=5+5=10$$ см.
Аналоги к этому заданию:
Задание 1025
Радиус $$OB$$ окружности с центром в точке $$O$$ пересекает хорду $$AC$$ в точке $$D$$ и перпендикулярен ей. Найдите длину хорды $$AC$$, если $$BD = 1$$, а радиус окружности равен $$5$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
