Задание 631
Задание 631
Даны четыре графика различных функций вида $$y=f(x)=ax^2+bx+c$$. На графиках отмечены по три точки с целыми координатами. Установите соответствие между графиками функций и значениями $$b$$. В ответе запишите последовательность цифр, соответствующих А, Б, В, Г, без пробелов, запятых и других разделительных символов.
ГРАФИКИ
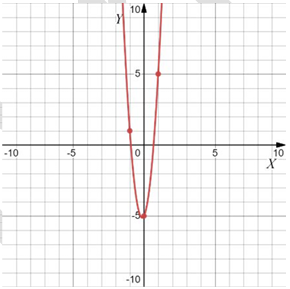
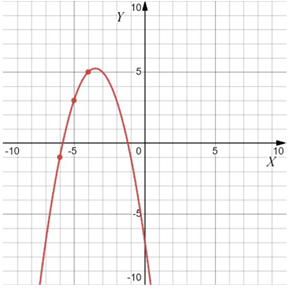
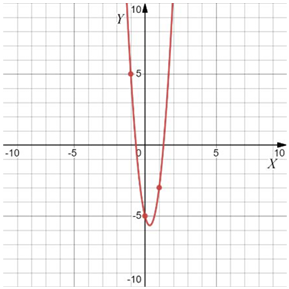
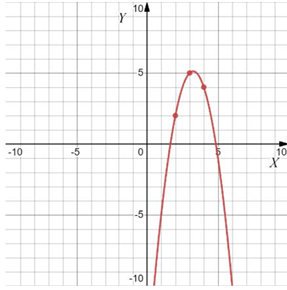
Варианты $$b$$:
1) $$b=-7$$
2) $$b=13$$
3) $$b=2$$
4) $$b=-4$$
| А | Б | В | Г |
А) ветви вверх, $$x_0<0\Rightarrow$$ т.к. $$x_0=-\frac{b}{2a}$$, $$a>0$$, то $$b>0$$
Б) ветви вниз $$(a<0), x_0<0\Rightarrow b<0$$
В) ветви вверх $$(a>0), x_0>0\Rightarrow b<0$$
Г) ветви вниз $$(a<0), x_0>0\Rightarrow b>0$$
При этом в пункте А имеем $$|a|$$ больше, чем $$|a|$$ в пункте Г. И при этом $$x_0$$ ближе, т.е. $$|b|$$ там меньше $$\Rightarrow$$ А-3; Г-2. Аналогично, Б-1; В-4.
Задание 700
Даны четыре графика функции вида $$y = ax^2 + bx + c$$. Найдите значения $$a$$. Установите соответствие между графиками функций и значениями $$a$$. В ответе запишите последовательность цифр, соответствующих А, Б, В, Г, без пробелов, запятых и других дополнительных символов.
ГРАФИКИ
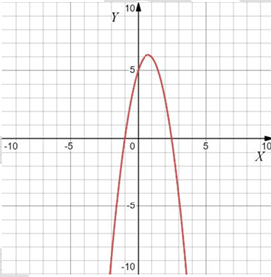
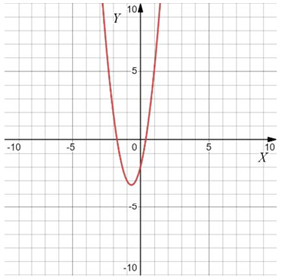
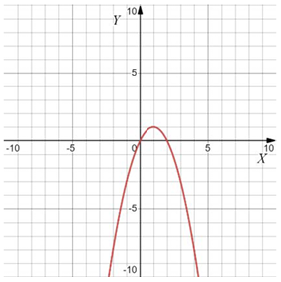
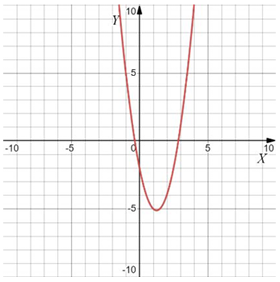
Варианты $$a$$:
1) $$-2$$
2) $$-1$$
3) $$3$$
4) $$2$$
| А | Б | В | Г |
Если ветви вверх, то $$a>0,$$ если вниз, то $$a<0.$$
Чем "уже" парабола, тем больше $$|a|.$$
Тогда: $$1324.$$