ОГЭ математика 2022. Разбор варианта Алекса Ларина № 293.

Найдите значение выражения $$24ab + 2(-2a + 3b)^2$$ при $$a = \sqrt{3}$$ и $$b = \sqrt{6}$$.

Решите систему уравнений: $$\left\{\begin{aligned} 3x + 2y = 8 \\ 4x - y = 7 \end{aligned}\right.$$ В ответе запишите значение выражения $$-4x_1 - 3y_1$$, где $$(x;y) = (x_1; y_1)$$ – решение системы.

В мешке содержатся жетоны с номерами от $$5$$ до $$54$$ включительно. Какова вероятность того, что извлечённый наугад из мешка жетон содержит двузначное число?

На рисунке изображён график функции $$y = ax^2 + bx + c$$. Установите соответствие между утверждениями и промежутками, на которых эти утверждения выполняются.mВ ответе укажите последовательность цифр, соответствующих А, Б, В, Г, без пробелов, запятых и других разделительных символов.

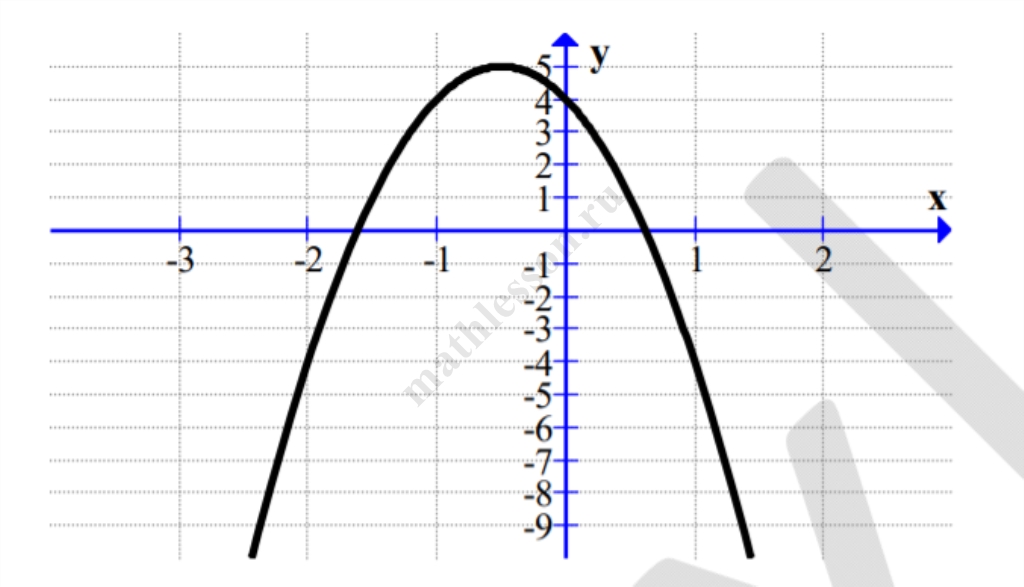
УТВЕРЖДЕНИЯ
А) Функция убывает на промежутке
Б) Функция возрастает на промежутке
В) Функция неотрицательна на промежутке
Г) Функция неположительна на промежутке

ПРОМЕЖУТКИ
1) $$\left[\frac{-\sqrt{5} + 1}{2}; \frac{\sqrt{5} - 1}{2}\right]$$
2) $$\left(-\infty; \frac{-\sqrt{5} + 1}{2}\right] \cup \left[\frac{\sqrt{5} - 1}{2}; +\infty\right)$$
3) $$\left(-\infty; -0,5\right]$$
4) $$\left[-0,5; +\infty\right)$$

В таблице под каждой буквой укажите соответствующий номер.

Решите неравенство $$-x^2 + x \ge 0$$. В ответе укажите номер правильного варианта ответа:
1) $$( -\infty;\ 0 ) \cup ( 1;\ +\infty )$$
2) $$[ 0;\ 1 ]$$
3) $$( 0;\ 1 )$$
4) $$( -\infty;\ 0 ] \cup [ 1;\ +\infty )$$

Лене надо подписать $$972$$ открытки. Ежедневно она подписывает на одно и то же количество открыток больше по сравнению с предыдущим днём. Известно, что за первый день Лена подписала $$20$$ открыток. Определите, сколько открыток было подписано за седьмой день, если вся работа была выполнена за $$18$$ дней.

В треугольнике $$ABC$$ проведены медиана и высота $$BM$$ и $$BH$$, причём точка $$H$$ лежит между $$M$$ и $$C$$. Известно, что $$AC = 79$$ и $$BC = BM$$. Найдите $$AH$$.

Прямая касается окружности в точке $$K$$. Точка $$O$$ — центр окружности. Хорда $$KM$$ образует с касательной угол, равный $$79^\circ$$. Найдите величину угла $$OMK$$. Ответ дайте в градусах.

Найдите площадь кругового сектора, если радиус круга равен $$3$$, а угол сектора равен $$120^\circ$$. В ответе укажите площадь, делённую на $$\pi$$.

На клетчатой бумаге изображён треугольник $$ABC$$. Известно, что $$AB =8$$. Найдите длину его высоты, опущенной на сторону $$AB$$.

Какие из следующих утверждений верны? Если верных утверждений несколько, запишите их номера в порядке возрастания без пробелов, запятых и других символов между ними.

1. Диагонали параллелограмма равны.
2. Площадь ромба равна произведению его стороны на высоту, проведённую к этой стороне.
3. Если две стороны и угол одного треугольника равны соответственно двум сторонам и углу другого треугольника, то такие треугольники равны.

Решите уравнение: $$2x^4 - 6x^3 - 19x^2 + 60x + 116 = 0$$

Две трубы, работая одновременно, наполняют бассейн за $$6$$ часов $$18$$ минут, а одна первая труба наполняет бассейн за $$9$$ часов. За сколько часов наполняет бассейн одна вторая труба?

Окружность, вписанная в треугольник $$ABC$$, касается сторон в точках $$M$$, $$N$$, $$P$$. Найдите углы треугольника $$ABC$$ , если углы треугольника $$MNP$$ равны $$56^{\circ}$$,$$58^{\circ}$$ и $$66^{\circ}$$.