ОГЭ математика 2022. Разбор варианта Алекса Ларина № 302.
Больше разборов на моем ютуб-канале
Задание 1-5
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 6
Найдите значение выражения $$\left(\frac{a}{3} + \frac{3}{a} + 2\right) \cdot \frac{1}{a + 3}$$ при $$a = 6$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 7
При каком значении $$x$$ значения выражений $$x - 7$$ и $$7x + 2$$ равны?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 8
Ниже представлены графики функций $$y = f(x)$$. Установите соответствие между графиками функций и формулами, которые их задают. В ответе укажите последовательность цифр, соответствующих А, Б, В, без пробелов, запятых и других разделительных символов.
ГРАФИКИ
ФОРМУЛЫ
1) $$y = -2x + 4$$
2) $$y = 2x - 4$$
3) $$y = 2x + 4$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 9
Длину окружности можно вычислить по формуле $$C = 2\pi R$$, где $$R$$ — радиус окружности. Пользуясь этой формулой, найдите радиус окружности, если её длина равна $$58\pi$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 10
Укажите неравенство, множеством решений которого является множество $$x \in ( -\infty;\ -8 ] \cup [ 8;\ +\infty )$$:
1) $$x^2 + 64 \ge 0$$
2) $$x^2 - 64 \le 0$$
3) $$x^2 - 64 \ge 0$$
4) $$x^2 + 64 \le 0$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 11
В амфитеатре $$16$$ рядов, причём в каждом следующем ряду на одно и то же число мест больше, чем в предыдущем. В четвёртом ряду $$23$$ места, а в восьмом ряду $$35$$ мест. Сколько мест в последнем ряду амфитеатра?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 12
В равнобедренном треугольнике $$ABC$$ с основанием $$AC$$ внешний угол при вершине $$C$$ равен $$123^\circ$$. Найдите величину угла $$ABC$$. Ответ дайте в градусах.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 14
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 15
Какие из следующих утверждений верны? Если верных утверждений несколько, запишите их номера в порядке возрастания без пробелов, запятых и других символов между ними.
- Все углы ромба равны.
- Если стороны одного четырёхугольника соответственно равны сторонам другого четырёхугольника, то такие четырёхугольники равны.
- Через любую точку, лежащую вне замкнутого круга, можно провести две касательные к окружности, ограничивающей этот круг.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 16
Решите неравенство: $$(x - 3)^2 \sqrt{5}(x - 3)$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


1) Перенесём всё в левую часть: $$(x - 3)^2 - \sqrt{5}(x - 3) < 0.$$ Вынесём общий множитель: $$(x - 3)\bigl((x - 3) - \sqrt{5}\bigr) < 0.$$ То есть $$(x - 3)(x - 3 - \sqrt{5}) < 0.$$
2) Нули выражения: $$x_1 = 3, x_2 = 3 + \sqrt{5}.$$ Отметим их на координатной прямой. Расставим знаки, которые принимает выражение $$(x - 3)(x - 3 - \sqrt{5})$$ на полученных интервалах:
Выражение отрицательно при: $$x \in (3;\, 3 + \sqrt{5}).$$
Задание 17
Постройте график функции $$y = \frac{(x^2 + 7x + 12)(x^2 - x - 2)}{x^2 + 5x + 4}$$. Определите, при каких значениях $$a$$ прямая $$y = a$$ имеет с графиком ровно одну общую точку.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


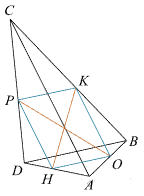
Задание 18
Найдите площадь выпуклого четырёхугольника с диагоналями $$8$$ и $$5$$, если отрезки, соединяющие середины его противоположных сторон, равны.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Пусть ABCD — данный четырёхугольник, O — середина стороны AB, K — середина стороны BC, P — середина стороны CD, H — середина стороны DA. Проведём диагонали AC и BD и отрезки OK, KP, PH и HO, последовательно соединяющие середины сторон четырёхугольника. Тогда, по свойству средней линии треугольника, отрезки OK и PH параллельны диагонали AC и равны её половине, а отрезки KP и HO параллельны диагонали BD и равны её половине. Поэтому OKPH — параллелограмм. А так как, по условию задачи, его диагонали KH и OP равны, то OKPH — прямоугольник, и угол OKP— прямой. Отсюда следует, что и угол между диагоналями AC и BD тоже прямой, и, следовательно, площадь четырёхугольника ABCD будет равна половине произведения его диагоналей, то есть $$\frac{1}{2}\cdot8\cdot5=20$$.
Задание 19
В параллелограмме $$ABCD$$ точка $$M$$ — середина стороны $$CD$$ . Известно, что $$MA=MB$$. Докажите, что данный параллелограмм — прямоугольник.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 20
В треугольнике $$ABC$$ на его медиане $$BM$$ отмечена точка $$K$$ так, что $$BK:KM=7:3$$. Прямая $$AK$$ пересекает сторону $$BC$$ в точке $$P$$. Найдите отношение площади треугольника $$BKP$$ к площади треугольника $$KPCM$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!