Задание 1051
Задание 1051
В параллелограмме $$ABCD$$ точка $$M$$ — середина стороны $$CD$$ . Известно, что $$MA=MB$$. Докажите, что данный параллелограмм — прямоугольник.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Аналоги к этому заданию:
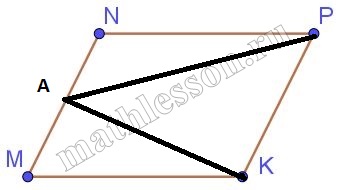
Задание 3743
В параллелограмме $$MNPK$$ точка $$A$$ — середина стороны $$MN$$. Известно, что $$AP=AK$$. Докажите, что данный параллелограмм — прямоугольник.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
1) По свойству параллелограмма: MN=NP. По условию AN=AM и AP=AK. Тогда треугольники ANP и AMK равны по трем сторонам, следовательно $$\angle ANP=\angle AMK=x$$
2) По свойству параллелограмма: $$\angle ANP+\angle AMK=180$$, следовательно $$\angle ANP=\angle AMK=90$$, тогда MNPK - прямоугольник
Задание 1744
В параллелограмме $$ABCD$$ точка $$E$$ — середина стороны $$AB$$ . Известно, что $$EC=ED$$. Докажите, что данный параллелограмм — прямоугольник.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 1855
В параллелограмме $$KLMN$$ точка $$E$$ – середина стороны $$KN$$. Известно, что $$EL=EM$$. Докажите, что данный параллелограмм – прямоугольник.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
