Задание 4058
Задание 4058
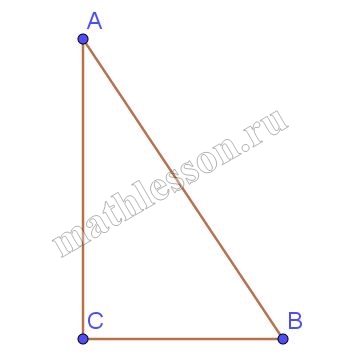
В треугольнике $$ABC$$ угол $$C = 90^\circ$$, $$AC = 12$$, $$\tan A = \frac{3}{4}$$. Найдите $$AB$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
$$tg A = \frac{CB}{AC}=\frac{3}{4}\Rightarrow $$$$CB=AC*tg A=9$$ По теореме Пифагора: $$AB=\sqrt{12^{2}+9^{2}}=15$$
Аналоги к этому заданию:
Задание 3889
В треугольнике $$ABC$$ угол $$C = 90^\circ$$, $$\tan A = 0,6$$, $$AC = 15$$. Найдите $$BC$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
$$tg \angle A = \frac{BC}{AC} = 0,6$$. Тогда $$BC = AC*0,6 =15 * 0,6 =9$$
Задание 4009
В треугольнике $$ABC$$ угол $$C$$ равен $$90^\circ$$, $$AC = 19,2$$, $$\tan A = \frac{7}{24}$$. Найдите $$AB$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
$$\tan A=\frac{7}{24}=\frac{CB}{19,2}$$; $$CB=\frac{7\cdot19,2}{24}=\frac{28}{5}=5,6$$; $$AB=\sqrt{19,2^{2}+5,6^{2}}=\sqrt{\frac{10000}{5^{2}}}=\frac{100}{5}=20$$
Задание 4484
В треугольнике $$ABC$$ угол $$C = 90^\circ$$, $$AC = 10$$, $$\tan A = 0,8$$. Найдите $$BC$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
tg A = CB/AC => CB=AC*tg A=10*0.8=8
Задание 3031
В треугольнике $$ABC$$ угол $$C = 90^\circ$$, $$AC = 8$$, $$\tan A = 0,75$$. Найдите $$BC$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
$$tg A=\frac{CB}{AC}\Rightarrow$$ $$CB=AC*tgA=0,75*8=6$$
Задание 3198
В треугольнике $$ABC$$ угол $$C = 90^\circ$$, $$AC = 12$$, $$\tan A = 0,75$$. Найдите $$BC$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
$$tg A=\frac{CB}{AC}\Rightarrow$$ $$CB=AC*tg A=12*0,75=9$$