Задание 1192

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

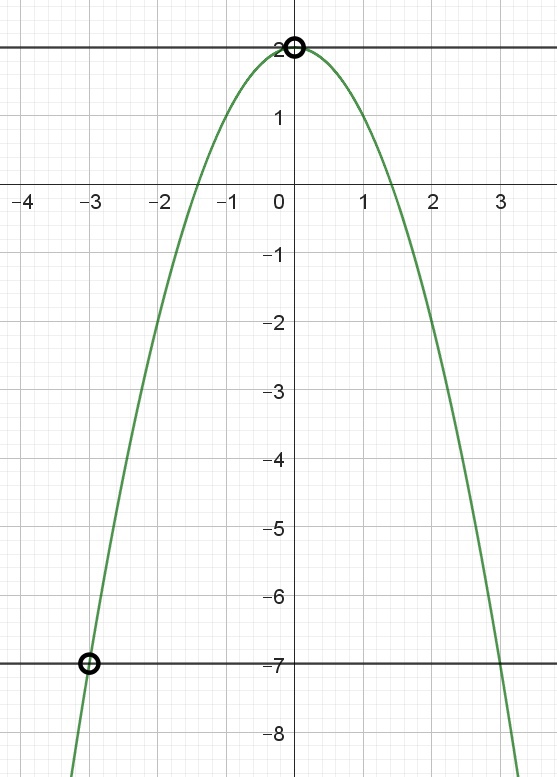
$$y=5-\frac{x^{4}-x^{3}}{x^{2}-x}$$

ОДЗ: $$x^{2}-x\neq0$$

$$\left\{\begin{matrix}x\neq0\\x\neq1\end{matrix}\right.$$

$$5-\frac{x^{4}-x^{3}}{x^{2}-x}=$$

$$=5-\frac{x^{2}(x^{2}-x)}{x^{2}-x}=5-x^{2}$$

$$y_{1}=5-x^{2}$$

То есть график первоначальной функции совпадает с графиком функции y₁ при учете ОДЗ. Построим график y₁ функции

Если прямая y=m проходит через оординаты 4 и 5, то получаем по одному пересечению, следовательно, их надо исключить, и тогда m будет принадлежать промежутку:

$$m\in(-\infty;4)\cup(4;5)$$

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

$$y=1-\frac{2x^{4}-x^{3}}{2x^{2}-x}=1-\frac{x^{3}(2x-1)}{x(2x-1)}$$$$\Rightarrow$$ $$y=\left\{\begin{matrix}1-x^{2}\\x\neq 0\\2x-1\neq 0\end{matrix}\right.\Leftrightarrow$$ $$y=\left\{\begin{matrix}1-x^{2}\\x \neq 0\\x\neq 0,5\end{matrix}\right.$$

Построим график данной функции (не забудем отметить пустыми точка (A и B) имеющиеся ограничения:

Видим, что прямая всегда будет пересекать в двух точках параболы (на области значений параболы) кроме тех случаев, когда она пройдет через точку А или В: $$m \in (-\infty;0,75)\cup (0,75; 1)$$

$$y=2-\frac{x^4+3x^3}{x^2+3x}=2-\frac{x^2(x^2+3x)}{x^2+3x}=2-x^2$$; $$x^2+3x\neq0$$

Получим: $$\left\{\begin{matrix} y=2-x^2\\ x\neq0;y\neq2\\ x\neq-3;y\neq-7 \end{matrix}\right.$$

$$m\in(-\infty;-7)\cup(-7;-2)$$ будет иметь 2 общие точки