ОГЭ математика 2023. Разбор варианта Алекса Ларина № 337.
Больше разборов на моем ютуб-канале
Задание 1-5
Квартиры
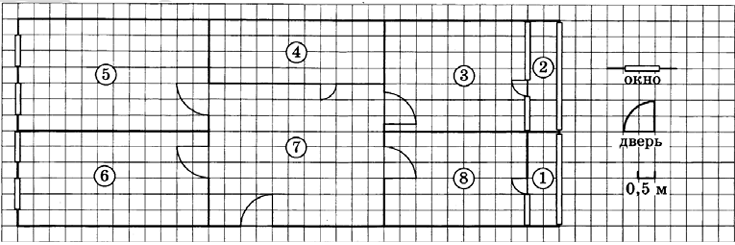
На рисунке (см. выше) изображён план трёхкомнатной квартиры в многоэтажном доме. Сторона каждой клетки на плане равна 0,5 м. Вход в квартиру находится в прихожей. Напротив входа располагается санузел. Справа от входа - гостиная и спальня, а слева - кухня и детская. В квартире есть две застеклённые лоджии. Площадь кухни равна 18 м2. Вход в детскую расположен напротив входа в гостиную. 1. Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу. В ответе запишите последовательность пяти цифр без пробелов, запятых и других разделительных символов.| Объекты | санузел | гостиная | детская | спальня | кухня |
|---|---|---|---|---|---|
| Цифры |
Вход в квартиру находится в прихожей (7). Напротив входа располагается санузел (4). В квартире есть две застеклённые лоджии (1 и 2).
Площадь кухни равна 18 квадратных метров ((6) $$S = 6\cdot0,5\cdot18\cdot0,5 = 18$$ м2), вход в детскую (5) расположен напротив входа в гостиную (3). Справа от входа — гостиная и спальня (8), а слева — кухня и детская.
Заполняем таблицу и записываем ответ.
Так как одна клетка равна 0,5 метра, а ширина лоджии = 6 клеток, следовательно остекление лоджии в спальне будет 3 метра.
Так как плитка 50 на 25 см, то есть 0,5 на 0,25 метров, значит, в одной клетке по 2 плитки.
Найдём площадь прихожей, она равна 99 клеток, или умножая на 2, 198 плиточек.
И, зная, что в одной упаковке 10 штук, мы $$\frac{198}{10}=19,8$$ упаковок, округляем, и получаем 20 упаковок.
$$S=ab$$
Считаем клетки:
$$12\cdot7=84$$
$$\frac{84}{4}=21$$ м2
Площадь спальни $$= 9\cdot6=54$$
Площадь кухни $$=12\cdot6=72$$
Пусть
72 - 100%
54 - x%
Тогда 54 = 75%
$$100\%-75\%=25\%$$
Задание 7
Известно, что $$2,6 a 2,8$$. Какому из нижеперечисленных чисел равно число $$a$$?
1) $$\sqrt{3}$$
2) $$\sqrt{7}$$
3) $$\sqrt{8}$$
4) $$\sqrt{12}$$
В ответе запишите номер правильного варианта ответа.
Учтём, что $$2,6=\sqrt{2,6^2}=\sqrt{5,76}$$; $$2,8=\sqrt{2,8^2}=\sqrt{7,24}\Rightarrow a=\sqrt{7}\Rightarrow 2$$
Задание 10
Даны четыре графика различных функций $$y=f(x)$$. Установите соответствие между графиками функций и формулами, которые их задают. В ответе запишите последовательность цифр, соответствующих А, Б, В, Г, без пробелов, запятых и других разделительных символов.
ГРАФИКИ
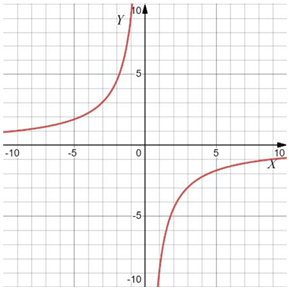
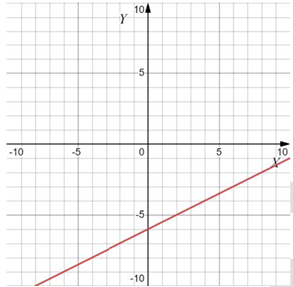
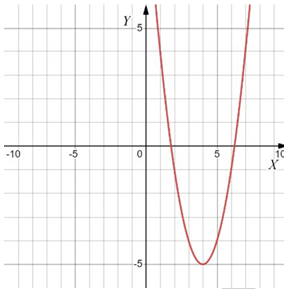
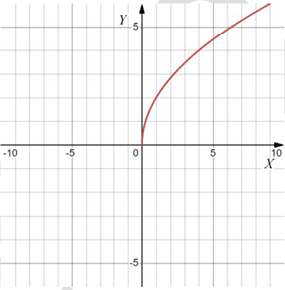
Формулы:
1) $$y = \frac{1}{2}x - 6$$
2) $$y = x^2 - 8x + 11$$
3) $$y = -\frac{9}{x}$$
4) $$y = 2\sqrt{x}$$
| А | Б | В | Г |
А) гипербола $$\Rightarrow y=-\frac{9}{x}\Rightarrow 3$$
Б) линейная функция $$\Rightarrow y=\frac{1}{2}x-6\Rightarrow 1$$
В) парабола $$\Rightarrow y=x^2-8x+11\Rightarrow 2$$
Г) ветвь параболы $$\Rightarrow y=2\sqrt{x}\Rightarrow 4$$
Задание 12
Решите неравенство: $$-x^2 + x \ge 0$$
1) $$( -\infty,\ 0 ) \cup ( 1,\ +\infty )$$
2) $$[ 0,\ 1 ]$$
3) $$( -\infty,\ 1 )$$
4) $$( -\infty,\ 0 ] \cup [ 1,\ +\infty )$$
Задание 13
В амфитеатре $$12$$ рядов. В первом ряду $$20$$ мест, а в каждом следующем на $$2$$ места больше, чем в предыдущем. Сколько всего мест в амфитеатре?
Воспользуемся формулой арифметической прогрессии.
$$a_1=20$$ мест, $$d = 2$$ места.
$$S_n=\frac{2a_1+d(n-1)}{2}n=\frac{2\cdot20+2(12-1)}{2}\cdot12=372$$
Задание 14
Сторона ромба $$ABCD$$ равна $$54$$, а один из углов этого ромба равен $$150^\circ$$. Найдите высоту ромба $$ABCD$$.
Высоту h ромба можно найти из прямоугольного треугольника с гипотенузой $$c=54$$ (длина стороны ромба) и острым углом $$\alpha=180^{\circ}-150^{\circ}=30^{\circ}$$. Высота лежит против острого угла в 30°, значит, она будет в 2 раза меньше гипотенузы:
$$h=c\cdot\sin30^{\circ}=54\cdot\frac{1}{2}=27$$
Задание 15
В окружность вписан равносторонний восьмиугольник $$ABCDEFGH$$. Найдите градусную меру угла $$ACE$$.
Равные хорды отсекают равные дуги. Т.е. каждая сторона отсекает дугу $$\frac{360^{\circ}}{8}=45^{\circ}.$$
$$\angle ACE$$ опирается на дугу, отсекаемую 4 сторонами, т.е. $$180^{\circ},$$ но угол вписанный $$\Rightarrow\angle ACE=\frac{180^{\circ}}{2}=90^{\circ}$$
Задание 16
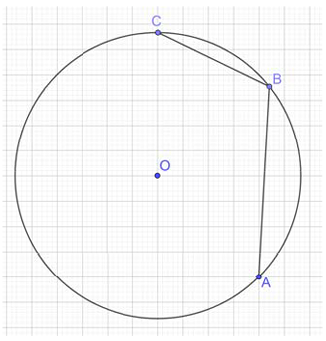
Согласно рисунку градусная мера центрального угла АОС равна $$45°+90° = 135°$$. Следовательно, дуга, на которую опирается вписанный в окружность угол АВС имеет градусную меру:
$$360°-135° = 225°$$.
По теореме о величине угла, вписанного в окружность, получаем, что градусная мера угла АВС:
$$\frac{225°}{2} = 112,5°$$.
Задание 17
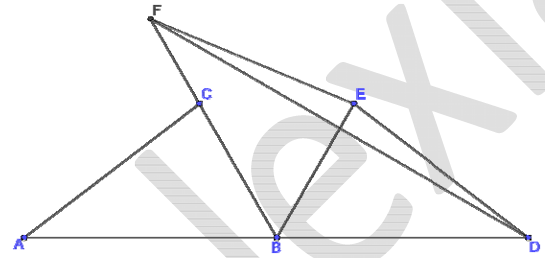
Из равенства треугольников ABC, DBE и FBE следует, что равны углы ABC, DBE и FBE, образующие развёрнутый угол, равный $$180°$$. Следовательно, каждый из этих углов равен
$$\frac{180°}{3} = 60°$$.
Угол DBF при вершине равнобедренного треугольника с основанием FD равен $$120°$$, так как составлен из двух углов DBE и FBE, каждый из которых равен $$60°$$. Значит, угол FDB при основании равнобедренного треугольника DBF:
$$\frac{180°-120°}{2} = 30°$$.
Задание 18
Какие из следующих утверждений верны? Если верных утверждений несколько, запишите их номера в порядке возрастания без пробелов, запятых и других разделительных символов.
- Площадь трапеции равна половине высоты, умноженной на разность оснований.
- Через любые две точки можно провести прямую.
- Через точку, не лежащую на данной прямой, можно провести единственную прямую, перпендикулярную данной прямой.
1) неверно, площадь трапеции равна половине высоты, умноженной на сумму оснований.
2) верно, это аксиома геометрии.
3) верно, это теорема планиметрии.
Задание 19
Решите систему уравнений: $$ \left\{ \begin{aligned} \frac{x + 5}{y - 3} = 0,\\ 2y^2 + x^2 - y = 40 \end{aligned} \right. $$
$$\left\{\begin{matrix} \frac{x+5}{y-3}=0\\ 2y^2+x^2-y=40 \end{matrix}\right.\Rightarrow\left\{\begin{matrix} x+5=0\\ y-3\neq0\\ 2y^2+x^2-y=40 \end{matrix}\right.\Rightarrow\left\{\begin{matrix} x=-5\\ 2y^2+25-y=40\\ y\neq3 \end{matrix}\right.\Leftrightarrow$$
$$\Leftrightarrow\left\{\begin{matrix} x=-5\\ 2y^2-y-15=0\\ y\neq3 \end{matrix}\right.\Rightarrow\left\{\begin{matrix} x=-5\\ y=-2,5 \end{matrix}\right.$$
$$2y^2-y-15=0$$
$$D=1+120=121$$
$$y_1=\frac{1+11}{4}=3$$ - не подходит
$$y_2=\frac{1-11}{4}=-2,5$$
Задание 20
Постройте график функции $$y = \frac{3{,}5|x| - 1}{|x| - 3{,}5x^2}$$. Определите, при каких значениях $$a$$ прямая $$y = ax$$ не имеет с графиком этой функции общих точек.
$$x = 0$$ – критическая точка, в ней подмодульное выражение меняет знак. Поэтому будем рассматривать два случая: когда $$x > 0$$ и $$x < 0$$.
1) При $$x > 0$$ функция примет такой вид
$$y=\frac{3,5x-1}{x-3,5x^2}=\frac{3,5x-1}{-x(-1+3,5x)}=-\frac{1}{x}$$
Графиком данной функции будет гипербола, к тому же, сразу определимся с ОДЗ. Т.к. у нас дана дробь, то ее знаменатель не может равняться нулю. Поэтому, икс не должен равняться 0 и 2/7 (х ≠ 0 и х ≠ 2/7).
Сразу найдем координаты точек, по которым будем чертить график.
| х | 0,5 | 1 | 2 |
| у | -2 | -1 | -0,5 |
Найдем координаты выколотой точки: если x ≠ 2/7, то y ≠ -3,5.
2) При $$х < 0$$ функция примет вид
$$y=\frac{-3,5x-1}{-x-3,5x^2}=\frac{-3,5x-1}{x(-1-3,5x)}=\frac{1}{x}$$
ОДЗ: х ≠ 0 и х ≠ -2/7.
Найдем координаты точек.
| х | -0,5 | -1 | -2 |
| у | -2 | -1 | -0,5 |
Найдем координаты выколотой точки: если x ≠ -2/7, то y ≠ -3,5.
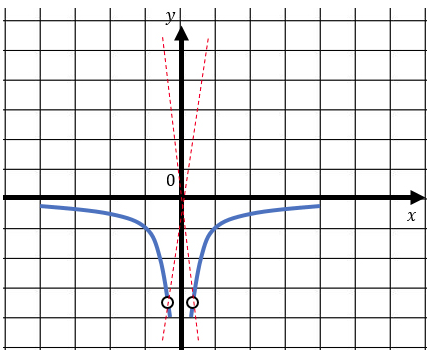
3) Теперь можно чертить график (синие кусочки гипербол).
$$y = kx$$ – прямая, проходящая под наклоном через начало координат (k – угловой коэффициент). И есть две потенциальные прямые, которые с нашим графиком не имеют общих точек (на координатной плоскости они отмечены красным цветом). Осталось лишь найти чему равен коэффициент k.
Обе прямые непременно должны проходить через выколотые точки. И логично предположить, что чтобы найти k надо в уравнение $$y = kx$$ подставить координаты этих выколотых точек. Это мы сейчас и сделаем.
Для точки (-2/7; -3,5)
$$-\frac{7}{2}=-\frac{2}{7}k;\; k=\frac{49}{4}=12,25$$
Для точки (2/7; -3,5)
$$-\frac{7}{2}=\frac{2}{7}k;\; k=-\frac{49}{4}=-12,25$$
И не стоит забывать, что при $$k = 0$$ прямая $$y = kx$$ превращается в прямую $$y = 0$$, которая совпадает с осью Ох. А, как известно, гипербола ее никогда не пересечет.
Таким образом, при $$k = ±12,25$$ и $$k = 0$$ прямая $$y = kx$$ не имеет с графиком общих точек.
Задание 21
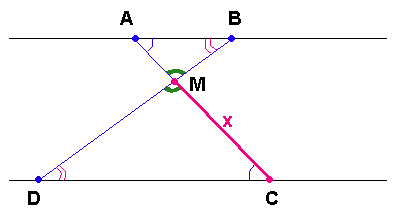
Отрезки $$AB$$ и $$DC$$ лежат на параллельных прямых, а отрезки $$AC$$ и $$BD$$ пересекаются в точке $$M$$. Найдите $$MC$$, если $$AB=18$$, $$DC=54$$, $$AC=48$$.
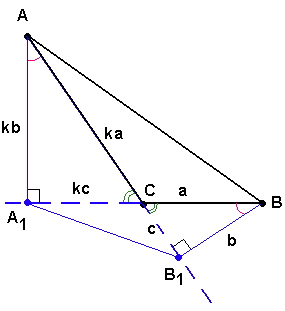
Задание 22
В треугольнике $$ABC$$ с тупым углом $$ACB$$ проведены высоты $$AA_{1}$$ и $$BB_{1}$$. Докажите, что треугольники $$A_{1}CB_{1}$$ и $$ACB$$ подобны.