ОГЭ математика 2023. Разбор варианта Алекса Ларина № 333.
Больше разборов на моем ютуб-канале
Задание 1-5
Квартиры
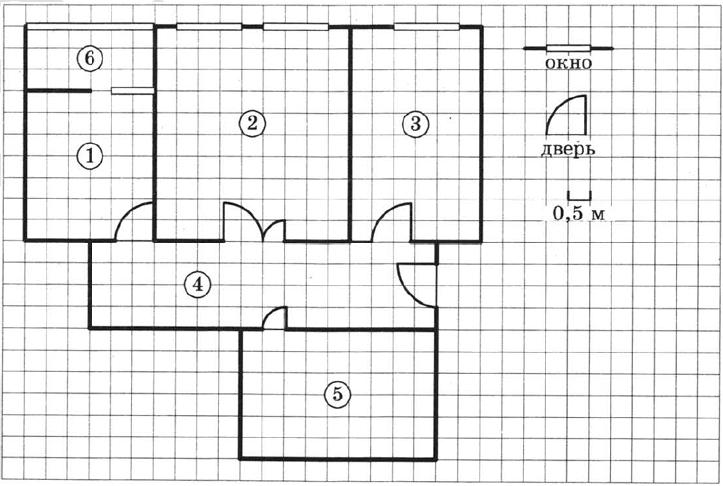
На рисунке изображён план двухкомнатной квартиры в многоэтажном жилом доме. Сторона каждой клетки на плане равна 0,5 м. Вход в квартиру находится в прихожей. Слева от входа расположен санузел, а справа - гостиная, кухня и спальня. На кухне есть выход в застеклённую лоджию. Их всех помещений в квартире гостиная занимает наибольшую площадь. 1. Для объектов, указанных в таблице, определите, какими цифрами они указаны на плане. Заполните таблицу. В ответе запишите последовательность пяти цифр без пробелов, запятых и других разделительных символов.| Объекты | спальня | санузел | кухня | гостиная | прихожая |
| Цифры |
По ходу прочтения задачи выясняется, что
4 - прихожая;
5 - санузел;
6 - лоджия;
1 - кухня;
2 - гостиная;
3 - спальня.
Заполним таблицу.
| Объекты | спальня | санузел | кухня | гостиная | прихожая |
| Цифры | 3 | 5 | 1 | 2 | 4 |
Окно в спальне занимает 3 клетки. Сторона клетки равна 0,5 м или 50 см.
Значит, ширина окна равна $$3\cdot50=150$$ см.
Лоджия занимает 18 клеток.
Т.к. сторона клетки равна 50 см, а размер плитки 25 х 25 см, то в одну клетку помещается 4 плитки.
Следовательно для лоджии потребуется $$18\cdot4=72$$ плитки.
Т.к. в упаковке 10 плиток, то упаковок потребуется $$\frac{72}{10}=7,2\approx8$$ упаковок.
Санузел занимает 54 клетки.
Площадь одной клетки $$0,5\cdot0,5=0,25$$ м2.
Найдем площадь санузла: $$54\cdot0,25=13,5$$ м2.
Гостиная занимает 90 клеток.
Спальная занимает 60 клеток.
Пусть спальня занимает 100%, а гостиная х%. Составим и решим пропорцию.
$$\frac{90}{60}=\frac{x}{100}$$
$$x=\frac{90\cdot100}{60}=150\%$$
Теперь посчитаем на сколько процентов гостиная больше спальни:
$$150\% - 100\%= 50\%.$$
Задание 7
Известно, что $$a b 0 c$$. Какое из следующих утверждений относительно этих чисел является верным?
1) $$a + b > 0$$
2) $$\frac{1}{b} > \frac{1}{c}$$
3) $$ab 0$$
4) $$(a - b)c 0$$
В ответе запишите номер правильного варианта ответа.
Пусть $$a=-2; b=-1; c=1.$$
$$a+b>0\Leftrightarrow -2-1>0$$ - неверно
$$\frac{1}{b}>\frac{1}{c}\Leftrightarrow \frac{1}{-1}>\frac{1}{1}$$ - неверно
$$ab<0\Leftrightarrow (-2)\cdot(-1)<0$$ - неверно
$$(a-b)\cdot c<0\Leftrightarrow (-2-(-1))\cdot1<0$$ - верно
Задание 9
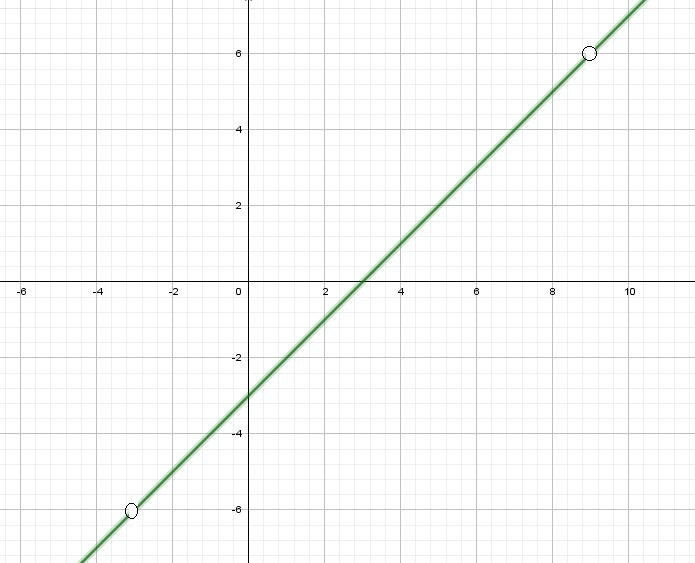
Ниже представлен график некоторой функции на отрезке $$[-5;\; 5]$$. Вне этого отрезка функция не определена. Установите соответствие между утверждениями для этой функции и их верностью. В ответе укажите последовательность цифр, соответствующих A, Б, В, Г, без пробелов, запятых и других разделительных символов.
ГРАФИКИ
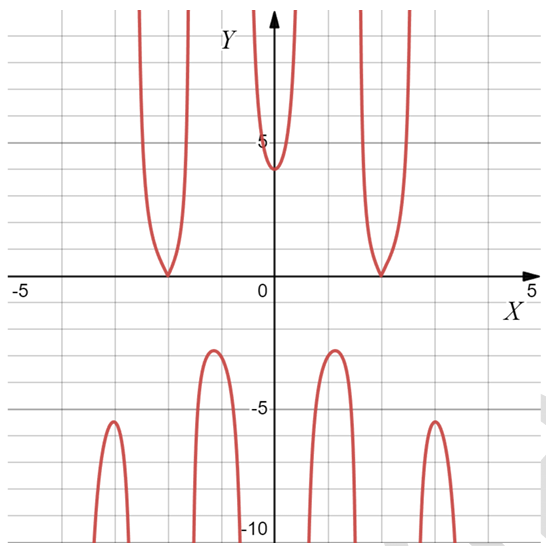
Утверждения
A) Функция непрерывна на отрезке $$[-5;\; 5]$$
Б) $$f(-1) > f(2)$$
В) На отрезке $$2 \leq x \leq 2{,}2$$ функция возрастает
Г) Функция имеет ровно 2 нуля функции
1) верно
2) неверно
| A | Б | В | Г |
А) нет, есть разрывы $$\Rightarrow 2$$
Б) $$f(-1)\approx-3,2; f(2)=0\Rightarrow f(-1)>f(2)$$ - нет $$\Rightarrow 2$$
В) да $$\Rightarrow 1$$
Г) да $$\Rightarrow 1$$
Задание 10
Площадь треугольника $$S$$ можно вычислить по формуле $$S = \frac{1}{2}ah$$, где $$a$$ — сторона треугольника, $$h$$ — высота, проведённая к этой стороне. Пользуясь этой формулой, найдите сторону $$a$$, если площадь треугольника равна $$28$$, а высота $$h$$ равна $$14$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


$$a=\frac{2S}{h}=\frac{2\cdot28}{14}=4$$
Задание 11
Решите систему неравенств:
$$\left\{\begin{aligned} x^2 \le 4 \\ x + 3 \ge 0 \end{aligned}\right.$$
1) $$( -\infty,\ 3 ]$$
2) $$( -\infty,\ 3 ] \cup [ 2;\ +\infty )$$
3) $$[ -2;\ 2 ]$$
4) $$[ -2;\ 3 ]$$
$$\left\{\begin{matrix} x^2\leq4\\ x+3\geq0 \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} x^2-4\leq0\\ x\geq-3 \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} x\in[-2;2]\\ x\geq-3 \end{matrix}\right.\Leftrightarrow x\in[-2;2]=3$$
Задание 12
За изготовление и установку нижнего железобетонного кольца колодца заплатили $$234\ 000$$ руб., а за каждое следующее кольцо платили на $$18\ 000$$ руб. меньше, чем за предыдущее. Кроме того, по окончании работы была выплачена премия $$360\ 000$$ руб. Средняя стоимость изготовления и установки одного кольца с учетом премии оказалась равна $$202\ 000$$ руб. Сколько колец было установлено?
Пусть за изготовление и установку всех колец заплатили Sn. Тогда
$$S_n=\frac{2a_1+(n-1)d}{2}n=\frac{2\cdot234-(n-1)\cdot18}{2}n=(243-9n)n.$$
Средняя стоимость установки одного кольца с учетом премии равна 202 рубля, а значит, $$\frac{360+S_n}{n}=202.$$ Получаем:
$$360+(243-9n)n=202n\Leftrightarrow 360+243n-9n^2=202n\Leftrightarrow$$
$$\Leftrightarrow 9n^2-41n-360=0\Leftrightarrow n=9$$
Следовательно, было установлено 9 колец.
Задание 13
Углы $$B$$ и $$C$$ треугольника $$ABC$$ равны соответственно $$61^{\circ}$$ и $$89^{\circ}$$. Найдите $$BC$$, если радиус окружности, описанной около треугольника $$ABC$$, равен $$10$$.
По сумме углов треугольника:
$$\angle A=180^{\circ}-61^{\circ}-89^{\circ}=30^{\circ}$$
По теореме синусов:
$$2R=\frac{BC}{\sin A}$$
$$BC=2R\cdot\sin A=2\cdot 10\cdot\sin 30^{\circ}=2\cdot 10\cdot 0.5=10$$
Задание 14
Радиус $$OB$$ окружности с центром в точке $$O$$ пересекает хорду $$MN$$ этой окружности в её середине — точке $$K$$. Найдите длину хорды $$MN$$, если $$KB = 1$$, а радиус окружности равен $$13$$.
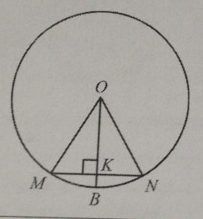
Построим радиусы ОН и ОМ.
Так как радиус ОВ перпендикулярен хорде МН, то треугольники ОКМ и ОКН прямоугольные.
В треугольниках ОКМ и ОКН катет ОК общий, а гипотенузы $$ОМ = ОН = R = 13$$ см.
Тогда прямоугольные треугольники ОКМ и ОКН равны по катету и гипотенузе, а значит $$КМ = КН.$$
Радиус $$ОВ = 13 = ВК + ОК = 1 + ОК.$$
$$ОК = 13 – 1 = 12$$ см.
По теореме Пифагора, из прямоугольного треугольника ОКН определим длину катета КН.
$$КН^2=ОН^2-ОК^2=169-144=25.$$
$$КН=5$$ см.
Тогда хорда $$МН=5+5=10$$ см.
Задание 15
Одна из сторон параллелограмма равна $$12$$, другая равна $$5$$, а один из углов — $$45^\circ$$. Найдите площадь параллелограмма, делённую на $$\sqrt{2}$$.
Площадь параллелограмма вычисляется по формуле:
$$S=a\cdot b\cdot\sin\alpha,$$ где а, b - стороны, $$\alpha$$ - угол между ними.
$$S=12\cdot5\cdot\sin45^{\circ}=60\cdot\frac{\sqrt{2}}{2}=30\sqrt{2}$$
$$\frac{S}{\sqrt{2}}=\frac{30\sqrt{2}}{\sqrt{2}}=30$$
Задание 16
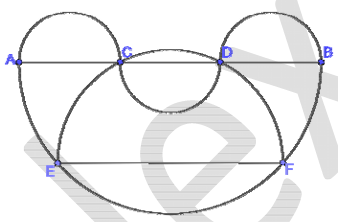
Дан полукруг диаметром $$AB$$ и три равных друг другу полукруга диаметрами $$AC$$, $$CD$$ и $$DB$$ (см. рис.). На полуокружности диаметром $$AB$$ взяты точки $$E$$ и $$F$$ так, что полуокружность диаметром $$EF$$ проходит через точки $$C$$ и $$D$$. Найдите площадь полукруга диаметром $$EF$$, если $$AC = \frac{4}{\sqrt{\pi}}$$.
Пусть O - середина EF, Q - середина CD, $$EO=OF=R, AC=CD=DB=r=\frac{4}{\sqrt{\pi}}.$$ В треугольнике EOQ по теореме Пифагора:
$$(\frac{3r}{2})^2=R^2+OQ^2 \Leftrightarrow OQ^2=\frac{9r^2}{4}-R^2. \quad \quad(1)$$
В треугольнике DQO по теореме Пифагора:
$$OQ^2+(\frac{r}{2})^2=R^2 \quad \quad(2)$$
Подставляя (1) в (2), получим:
$$\frac{9r^2}{4}-R^2+(\frac{r}{2})^2=R^2 \Leftrightarrow R^2= \frac {5r^2}{4} \quad \quad(3)$$
С учётом (3) искомая площадь S:
$$S=\frac {\pi R^2}{2} = \frac{\pi}{2} \cdot \frac {5r^2}{4} = \frac{5\pi}{8} \cdot \frac{16}{\pi} =10.$$
Задание 17
Какие из следующих утверждений верны? Если верных утверждений несколько, запишите их номера в порядке возрастания без пробелов, запятых и других разделительных символов.
- Вертикальные углы равны.
- Две окружности пересекаются, если радиус одной окружности больше радиуса другой окружности.
- Диагонали трапеции пересекаются и делятся точкой пересечения пополам.
1) верно
2) неверно, т. к. для того, чтобы утверждать, пересекаются окружности или нет, нужно ещё знать взаимное положение их центров.
3) неверно, диагонали ромба пересекаются и делятся точкой пересечения пополам.
Задание 18
При каких целых значениях $$n$$ выражение $$\frac{2n - 3}{n + 1}$$ является целым числом?
$$\frac{2n-3}{n+1}=\frac{2n+2-2-3}{n+1}=\frac{2n+2}{n+1}-\frac{5}{n+1}\Leftrightarrow 2-\frac{5}{n+1}$$
Так как $$n\in Z,$$ то $$\frac{5}{n+1}$$ должно тоже быть целым, чтобы $$\frac{2n-3}{n+1}\in Z.$$
Тогда $$n+1$$ делит нацело 5:
$$\left[\begin{matrix} n+1=\pm1\\ n+1=\pm5 \end{matrix}\right.\Leftrightarrow\left[\begin{matrix} n=0;-2\\ n=-6;4 \end{matrix}\right.$$
Задание 19
Имеется два сплава с разным содержанием золота: в первом содержится $$50 \%$$, а во втором — $$80 \%$$ золота. В каком отношении надо взять первый и второй сплавы, чтобы получить из них новый сплав, содержащий $$55 \%$$ золота?
1 сплав $$x$$ кг меди $$50\% = 0,5x$$
2 сплав $$y$$ кг меди $$80\% = 0,8y$$
$$1+2$$ сплав $$(x+y)$$ кг меди $$0,5x + 0,8y$$ или $$55\% = 0,55(x+y)$$
$$0,5x + 0,8y = 0,55(x+y)$$
$$0,5x + 0,8y = 0,55x + 0,55y$$
$$0,5x - 0,55x = 0,55y - 0,8y$$
$$-0,05x =-0,25y$$
$$5x = 25y$$
$$x = 5y$$
$$x = 5$$ (1 сплав)
$$y=1$$ (2 сплав)
$$\frac{x}{y}=\frac{5}{1}$$
Задание 20
Постройте график функции $$y = \frac{(x - 9)(x^2 - 9)}{x^2 - 6x - 27}$$. Найдите все значения $$a$$, при каждом из которых прямая $$y = ax$$ не имеет с графиком данной функции ни одной общей точки.
Область определения функции: функция существует, если знаменатель дроби не обращается в нуль, т.е. $$x^2-6x-27\neq0$$
$$(x-3)^2-36\neq0$$
$$(x-3-6)(x-3+6)\neq0$$
$$(x-9)(x+3)\neq0$$
$$x_1\neq9$$
$$x_2\neq-3$$
Упростим функцию: $$y=\frac{(x-9)(x-3)(x+3)}{(x+3)(x-9)}=x-3$$
Получили линейную функцию; графиком линейной функции является прямая, проходящая через точки $$(0;-3), (3;0).$$
Графики функций не имеют общих точек, если $$y=kx$$ проходит через выколотые точки, т.е. через точки $$(9;6), (-3;-6)$$
Подставляя координаты, получим:
$$6=9k\Rightarrow k=\frac{2}{3}$$
$$-6=-3k\Rightarrow k=2$$
Решим теперь уравнение $$kx=x-3\Rightarrow x=\frac{3}{1-k}$$
Очевидно, что при $$k=1$$ уравнение решений не имеет, а следовательно, графики функций при k=1 не имеют общих точек.
Ответ: $$\frac{2}{3}; 1; 2.$$
Задание 21
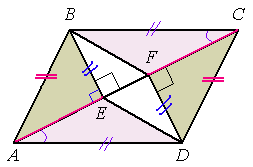
В параллелограмме $$ABCD$$, проведены перпендикуляры $$BE$$ и $$DF$$ к диагонали $$AC$$. Докажите, что $$BFDE$$ — параллелограмм.