ОГЭ математика 2022. Разбор варианта Алекса Ларина № 297.
Больше разборов на моем ютуб-канале
Задание 1-5
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 6
Найдите значение выражения $$\frac{9x - 25y}{3\sqrt{x} - 5\sqrt{y}} - 2\sqrt{y}$$, если $$\sqrt{x} + \sqrt{y} = 6$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 7
Решите уравнение: $$-4x + 8 = 10$$. В ответе запишите корень этого уравнения.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 8
В группе из $$20$$ российских туристов несколько человек владеют иностранными языками. Из них пятеро говорят только по‐английски, трое — только по‐французски, двое — по‐французски и по‐английски. Какова вероятность того, что случайно выбранный турист говорит по‐французски?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


В группе из 20 российских туристов французским языком владеют 3 (говорят только по-французски) + 2 (говорят по-французски и по-английски) = 5 человек.
Вероятность того, что случайно выбранный турист говорит по-французски = количество туристов, которые владеют французским языком : общее количество туристов:
$$P(A)=\frac{5}{20}=0,25$$
Задание 9
Ниже представлены графики функции вида $$y = ax^2 + c$$. Установите соответствие между графиками и знаками коэффициентов $$a$$ и $$c$$. В ответе укажите последовательность цифр, соответствующих А, Б, В, Г, без пробелов, запятых и других разделительных символов.
ГРАФИКИ
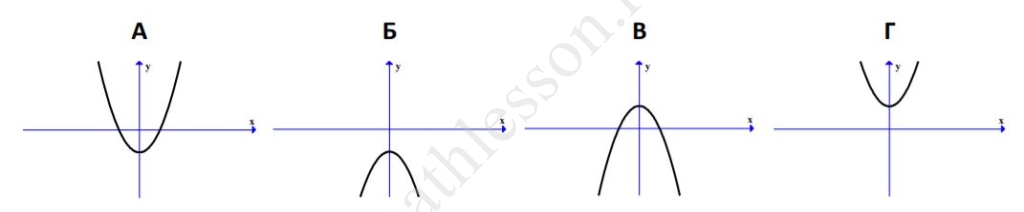
КОЭФФИЦИЕНТЫ
1) $$a<0$$, $$c<0$$
2) $$a<0$$, $$c>0$$
3) $$a>0$$, $$c<0$$
4) $$a>0$$, $$c>0$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 10
Закон всемирного тяготения можно записать в виде $$F = \gamma \frac{m_1 m_2}{r^2}$$, где $$F$$ — сила притяжения между телами (в ньютонах), $$m_1$$ и $$m_2$$ — массы тел (в килограммах), $$r$$ — расстояние между центрами масс тел (в метрах), а $$\gamma$$ — гравитационная постоянная, равная $$6,67 \cdot 10^{-11}$$ Н·м²/кг². Пользуясь этой формулой, найдите массу тела $$m_1$$ в килограммах, если $$F = 4,002$$ Н, $$m_2 = 4 \cdot 10^9$$ кг, $$r = 2$$ м.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 11
В угол величиной $$70^\circ$$ вписана окружность, которая касается его сторон в точках $$A$$ и $$B$$. На большей из дуг $$AB$$ этой окружности выбрали точку $$C$$. Найдите градусную меру угла $$ACB$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 12
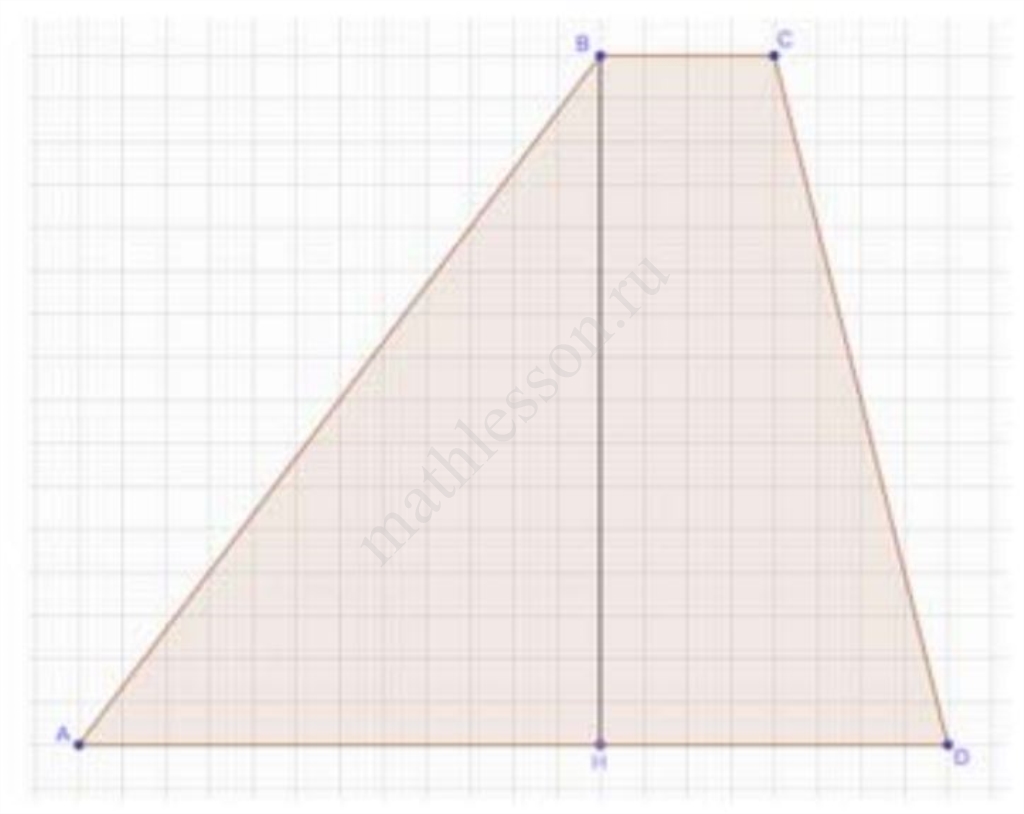
В треугольнике $$ABC$$ отмечены середины $$M$$ и $$N$$ сторон $$BC$$ и $$AC$$ соответственно. Площадь треугольника $$CNM$$ равна $$12$$. Найдите площадь четырёхугольника $$ABMN$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 13
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 14
Какие из следующих утверждений верны? Если верных утверждений несколько, запишите их номера в порядке возрастания без пробелов, запятых и других символов между ними.
- Один из углов треугольника всегда не превышает $$60^{\circ}$$ градусов.
- Диагонали трапеции пересекаются и делятся точкой пересечения пополам.
- Все диаметры окружности равны между собой
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 15
Решите уравнение: $$(x - 1)(x^2 + 4x + 4) = 4(x + 2)$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


1) Заметим: $$x^2 + 4x + 4 = (x + 2)^2.$$ Тогда: $$(x - 1)(x + 2)^2 = 4(x + 2).$$ Вынесем общий множитель: $$(x + 2)\bigl((x - 1)(x + 2) - 4\bigr) = 0.$$ Отсюда: $$x + 2 = 0,$$ или $$(x - 1)(x + 2) - 4 = 0.$$
2) Первый корень: $$x = -2.$$
3) Решим второе уравнение: $$(x - 1)(x + 2) - 4 = 0,$$ $$x^2 + x - 2 - 4 = 0,$$ $$x^2 + x - 6 = 0.$$ Дискриминант: $$D = 1^2 - 4\cdot 1\cdot(-6) = 1 + 24 = 25.$$ Корни: $$x_{1,2} = \frac{-1 \pm 5}{2},$$ $$x_1 = 2,\quad x_2 = -3.$$
Задание 16
Первый рабочий за час делает на $$5$$ деталей больше, чем второй, и выполняет заказ, состоящий из $$200$$ деталей, на $$2$$ часа быстрее, чем второй рабочий, выполняющий такой же заказ. Сколько деталей в час делает второй рабочий?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 17
Постройте график функции $$y = -4 - \frac{x^4 + x^3}{x^2 + x}$$ и определите, при каких значениях $$m$$ прямая $$y = m$$ имеет с графиком ровно две общие точки.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 18
Найдите отношение двух сторон треугольника, если его медиана, выходящая из их общей вершины, образует с этими сторонами углы в $$30^{\circ}$$ и $$90^{\circ}$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


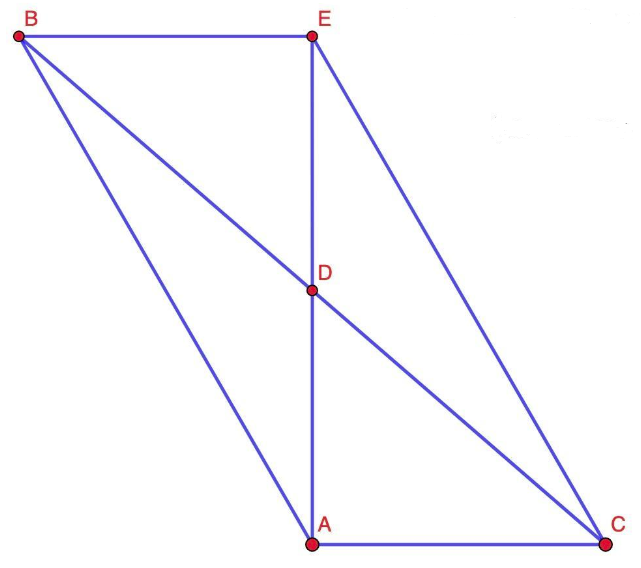
На продолжении AD за точку D отложим DE=AD, тогда ABEC - параллелограмм (по признаку) $$\Rightarrow BE||AC;$$
$$BE=AC$$ и $$\angle EAC=\angle BEA=90^{\circ}$$ (как накрест лежащие), $$\angle BAE=30^{\circ}\Rightarrow$$
$$\Rightarrow BE=\frac{1}{2}AB\Rightarrow AC=\frac{1}{2}AB\Rightarrow \frac{AC}{AB}=\frac{1}{2}$$
Задание 19
Окружности с центрами в точках $$O_{1}$$ и $$O_{2}$$ не имеют общих точек, и ни одна из них не лежит внутри другой. Внутренняя общая касательная к этим окружностям делит отрезок, соединяющий их центры, в отношении $$m:n$$. Докажите, что диаметры этих окружностей относятся как $$m:n$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 20
В треугольнике $$ABC$$ известны длины сторон $$AB=60$$, $$AC=80$$, точка $$O$$ - центр окружности, описанной около треугольника $$ABC$$. Прямая $$BD$$, перпендикулярная прямой $$AO$$, пересекает сторону $$AC$$ в точке $$D$$. Найдите $$CD$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!