ОГЭ математика 2022. Разбор варианта Алекса Ларина № 296.
Больше разборов на моем ютуб-канале
Задание 1-5
Шины
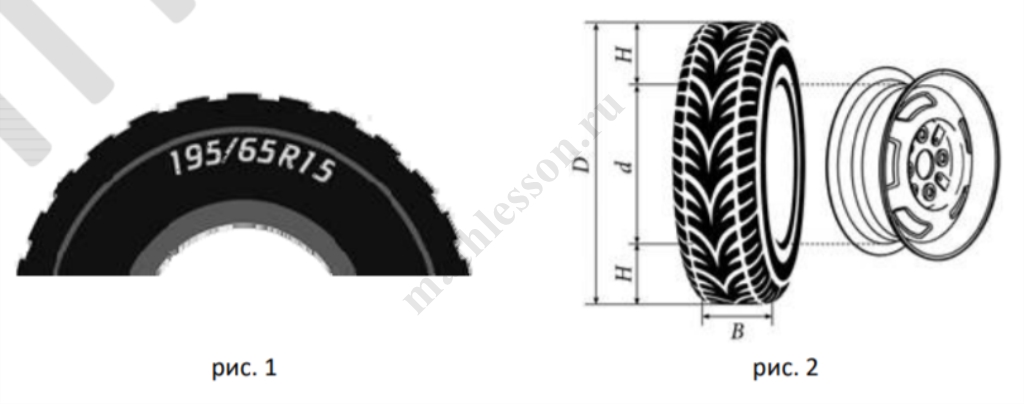
Автомобильное колесо, как правило, представляет собой металлический диск с установленной на него резиновой шиной (см. рис. 1 и рис. 2 выше). Диаметр диска совпадает с диаметром внутреннего отверстия в шине.
Для маркировки автомобильных шин применяется единая система обозначений. Например, 195/65 R15 (рис. 1).
Первое число (число 195 в приведённом примере) обозначает ширину шины в миллиметрах (параметр B на рисунке 2).
Второе число (число 65 в приведённом примере) — процентное отношение высоты боковины (параметр H на рисунке 2) к ширине шины, то есть $$100\cdot \frac{H}{B}$$.
Последующая буква обозначает тип конструкции шины. В данном примере буква R означает, что шина радиальная, то есть нити каркаса в боковине шины расположены вдоль радиусов колеса. На всех легковых автомобилях применяются шины радиальной конструкции.
За обозначением типа конструкции шины идёт число, указывающее диаметр диска колеса d в дюймах (в одном дюйме 25,4 мм). Таким образом, общий диаметр колеса D легко найти, зная диаметр диска и высоту боковины. Возможны дополнительные маркировки, обозначающие допустимую нагрузку на шину, сезонность использования, тип дорожного покрытия и другие параметры. Завод производит автомобили определённой модели и устанавливает на них колёса с шинами маркировки 265/60 R18.
1. Завод допускает установку шин с другими маркировками. В таблице показаны разрешённые размеры шин.
| Ширина шины (мм) | Диаметр диска (дюймы) | |||
| 17 | 18 | 19 | 20 | |
| 245 | 245/70 | – | – | – |
| 255 | 255/70 | 255/65 | – | – |
| 265 | 265/65 | 265/60, 265/65 | – | – |
| 275 | 275/65 | 275/60 | 275/55 | 275/50 |
| 285 | – | 285/60 | 285/55 | 285/50 |
Шины какой наибольшей ширины (в мм) можно устанавливать на автомобиль, если диаметр диска равен 17 дюймам?
2. На сколько миллиметров радиус колеса с шиной с маркировкой 245/70 R17, меньше радиуса колеса с шиной с маркировкой 275/65 R17?
3. Найдите диаметр (в см) колеса автомобиля, выходящего с завода.
4. На сколько миллиметров увеличится диаметр колеса, если заменить шины, установленные на заводе, шинами с маркировкой 285/50 R20?
5. На сколько процентов увеличится пробег автомобиля при одном обороте колеса, если заменить шины, установленные на заводе, шинами с маркировкой 285/50 R20? Ответ округлите до десятых.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 6
Найдите значение выражения $$\frac{7,2-6,1}{2,2}$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 8
Найдите значение выражения $$\frac{a(b - 3a)^2}{3a^2 - ab} - 3a$$ при $$a = 2,18$$, $$b = -5,6$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 9
Решите систему уравнений: $$\left\{\begin{aligned} 3x + 2y = 8 \\ 4x - y = 7 \end{aligned}\right.$$ В ответе запишите $$x + y$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


$$\left\{\begin{matrix} 3x+2y=8\\ 4x-y=7\quad |\cdot2 \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} 3x+2y=8\quad (1)\\ 8x-2y=14\quad (2) \end{matrix}\right.$$
$$(1) + (2):$$
$$11x=22$$
$$x=2,$$ тогда $$y=1$$
$$x+y=1+2=3$$
Задание 10
В чемпионате по футболу участвуют $$16$$ команд, которые жеребьёвкой распределяются на $$4$$ группы: $$A$$, $$B$$, $$C$$ и $$D$$. Какова вероятность того, что команда России не попадает в группу $$A$$?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


В каждой группе будет по $$\frac{16}{4}=4$$ команды.
Вероятность того, что команда из России попадет в группу А, равна $$\frac{4}{16}=\frac{1}{4}=0,25.$$
Следовательно, вероятность обратного события, что команда из России не попадет в группу А, равна $$1 - 0,25 = 0,75.$$
Задание 11
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 12
Решите неравенство $$(2x - 5)(x + 3) \ge 0$$. В ответе укажите номер правильного варианта ответа:
1) $$( -\infty;\ -3 );\ ( \frac{5}{2};\ +\infty )$$
2) $$( -\infty;\ -3 ];\ [ \frac{5}{2};\ +\infty )$$
3) $$[ -3;\ -\frac{5}{2} ]$$
4) $$( -3;\ -\frac{5}{2} )$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 13
У Кати есть попрыгунчик (каучуковый шарик). Она со всей силы бросила его об асфальт. После первого отскока попрыгунчик подлетел на высоту $$400$$ см, а после каждого следующего отскока от асфальта подлетал на высоту в два раза меньше предыдущей. После какого по счёту отскока высота, на которую подлетит попрыгунчик, станет меньше $$20$$ см?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Задание 14
Один угол параллелограмма в $$35$$ раз больше другого. Найдите меньший угол. Ответ дайте в градусах.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 15
Отрезки $$AB$$ и $$CD$$ являются хордами окружности. Найдите расстояние от центра окружности до хорды $$CD$$, если $$AB=40$$, $$CD=42$$, а расстояние от центра окружности до хорды $$AB$$ равно $$21$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 16
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 17
Какие из следующих утверждений верны? Если верных утверждений несколько, запишите их номера в порядке возрастания без пробелов, запятых и других символов между ними.
- Точка касания двух окружностей равноудалена от центров этих окружностей.
- В параллелограмме есть два равных угла
- Площадь прямоугольного треугольника равна произведению длин его катетов.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 18
Теплоход проходит по течению реки до пункта назначения $$280$$ км и после стоянки возвращается в пункт отправления. Найдите скорость течения, если скорость теплохода в неподвижной воде равна $$24$$ км/ч, стоянка длится $$15$$ часов, а в пункт отправления теплоход возвращается через $$39$$ часов. Ответ дайте в км/ч.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 19
Найдите наибольшее значение выражения $$\frac{x^3 - y}{x^2 + 1} - \frac{x^2y - x}{x^2 + 1}$$, если $$x$$ и $$y$$ связаны соотношением $$y = x^2 + x - 4$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 20
В трапеции $$ABCD$$ основание $$AD$$ вдвое больше основания $$BC$$ и вдвое больше боковой стороны $$CD$$. Угол $$ADC$$ равен $$60^{\circ}$$, сторона $$AB$$ равна $$4$$. Найдите площадь трапеции.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 21
Докажите, что отрезок, соединяющий середины оснований трапеции, делит её на две равные по площади части.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 22
В окружности с центром в точке $$O$$ проведены две хорды $$AB$$ и $$CD$$. Прямые $$AB$$ и $$CD$$ перпендикулярны и пересекаются в точке $$M$$, лежащей вне круга, ограниченного этой окружностью. При этом $$AM=36$$, $$BM=6$$, $$CD=4\sqrt{46}$$. Найдите $$OM$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!