ОГЭ математика 2023. Разбор варианта Алекса Ларина № 335.
Больше разборов на моем ютуб-канале
Задание 1-5
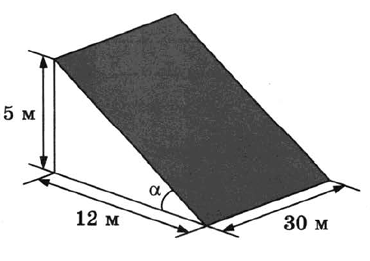
Террасы
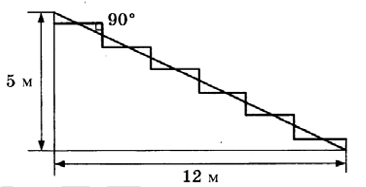
В горных районах, особенно в южных широтах с влажным климатом, земледельцы на склонах гор устраивают террасы (см. рис. выше). Земледельческие террасы - это горизонтальные площадки, напоминающие ступени. Во время дождя вода стекает с верхних террас вниз по специальным каналам. Поэтому почва на террасах не размывается и урожай не страдает. Медленный сток воды с вершины склона вниз с террасы на террасу позволяет выращивать даже влаголюбивые культуры. В Юго-Восточной Азии террасное земледелие широко применяется для производства риса, а в Средиземноморье - для выращивания винограда и оливковых деревьев. Возделывание культур на террасах повышает урожайность, но требует тяжёлого ручного труда. Земледелец владеет несколькими участками, один из которых расположен на склоне холма. Ширина участка равна 30 м, а верхняя точка находится на высоте 5 м от подножия (см. рис. ниже). 1. Земледелец на расчищенном склоне холма (ещё не террасированном) выращивал мускатный орех. Какова была площадь (в м2), отведённая под посевы? 2. Затем земледелец решил устроить террасы на своём участке (см. рисунок ниже), чтобы выращивать рис, пшено или кукурузу. Строительство террас возможно, если угол склона (уклон) не больше 50% (тангенс угла наклона, умноженный на 100%). Сколько процентов составляет уклон? Ответ округлите до десятых. 3. На сколько процентов сократилась посевная площадь после того, как земледелец устроил террасы? Ответ округлите до десятых. 4. Земледелец получает 800 г бурого риса с одного квадратного метра засеянной площади уже террасированного участка. При шлифовке из бурого риса получается белый рис, но при этом теряется 22% массы. Сколько килограммов белого риса получит земледелец со всего своего террасированного участка? 5. В таблице дана урожайность культур, которые может засеять земледелец на своём террасированном участке. За год обычно собирается два урожая: летом и осенью. По данным таблицы посчитайте наибольшее число килограммов урожая, которое может собрать земледелец с участка за один год, если он может засевать разные культуры.| Урожай | Урожайность риса (г/м2) | Урожайность кукурузы (г/м2) | Урожайность пшена (г/м2) |
|---|---|---|---|
| Первый (июнь) | 600 | 1200 | - |
| Второй (сентябрь) | 800 | - | 300 |
Задание 7
Известно, что $$a > b$$. Какое из следующих утверждений относительно этих чисел является верным при любых возможных значениях $$a$$ и $$b$$?
1) $$a - b > -10$$
2) $$a > 32$$
3) $$b - a -4$$
4) $$a - b 20$$
В ответе запишите номер правильного варианта ответа.
1) $$a-b>-10\Rightarrow a>-10+b$$ - верно
2) $$b-a>32\Rightarrow -a>32-b\Rightarrow a<-32+b$$ - неверно
3) $$b-a<-4\Rightarrow -a<-4-b\Rightarrow a>b+4$$ - неверно
4) $$a-b<20\Rightarrow a<20+b$$ - неверно
Задание 9
Решите систему уравнений: $$\left\{\begin{aligned} x^2 + 3x + y^2 = 2 \\ x^2 + 3x - y^2 = -6 \end{aligned}\right.$$ В ответе запишите значение выражения $$10x_1 - 5y_1 + 2x_2 - 6y_2 - 8x_3 - 9y_3 - 2y_4$$, где $$(x_i; y_i)$$ — решение этой системы, причём $$x_i \le x_{i+1}$$ и $$y_i y_{i+1}$$, если $$x_i = x_{i+1}$$.
$$\left\{\begin{matrix} x^2+3x+y^2=2\\ x^2+3x-y^2=-6 \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} 2x^2+6x=-4\\ x^2+3x-y^2=-6 \end{matrix}\right.$$
$$x^2+3x+2=0\Rightarrow\left[\begin{matrix} x_1=-2\\ x_2=-1 \end{matrix}\right.$$
При $$x=-2: 4-6-y^2=-6\Rightarrow y^2=4\Rightarrow y=\pm2$$
При $$x=-1: 1-3-y^2=-6\Rightarrow y^2=4\Rightarrow y=\pm2$$
Получим: $$(-2;-2); (-2;2); (-1;-2); (-1;2)$$
Тогда: $$10\cdot(-2)-5\cdot(-2)+2\cdot(-2)-6\cdot(-2)-8\cdot(-1)-9\cdot(-2)-2\cdot2=-4$$
Примечание от наборщика.
Ларин - чудак, такое детям в простом варианте не дают. Маразм крепчал. x2
Задание 10
Даны четыре графика функции вида $$y = ax^2 + bx + c$$. Найдите значения $$a$$. Установите соответствие между графиками функций и значениями $$a$$. В ответе запишите последовательность цифр, соответствующих А, Б, В, Г, без пробелов, запятых и других дополнительных символов.
ГРАФИКИ
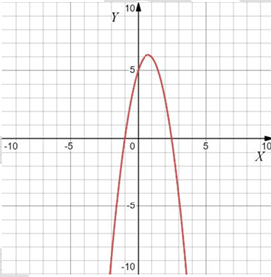
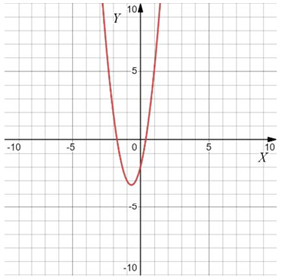
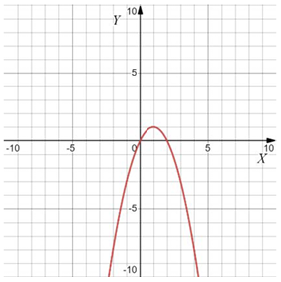
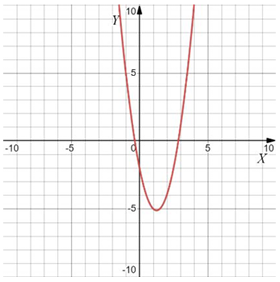
Варианты $$a$$:
1) $$-2$$
2) $$-1$$
3) $$3$$
4) $$2$$
| А | Б | В | Г |
Если ветви вверх, то $$a>0,$$ если вниз, то $$a<0.$$
Чем "уже" парабола, тем больше $$|a|.$$
Тогда: $$1324.$$
Задание 11
Расстояние $$s$$ (в метрах) до места удара молнии можно приближённо вычислить по формуле $$s = 330t$$, где $$t$$ — количество секунд, прошедших между вспышкой молнии и ударом грома. Определите, на каком расстоянии от места удара молнии находится наблюдатель, если $$t = 22$$ с. Ответ дайте в километрах.
$$s=330\cdot22=7260$$ м = $$7,26$$ км
Задание 12
Решите систему неравенств:
$$\left\{\begin{aligned} \frac{6 - 3x}{4 + (9 - 2x)^2} \ge 0 \\ 5 - 8x \le 23 - 5x \end{aligned}\right.$$
1) $$[ -6;\ 2 ]$$
2) $$[ 2;\ \frac{7}{2} ) \cup ( \frac{11}{2};\ +\infty )$$
3) $$[ 2;\ \frac{7}{2} )$$
4) $$( -\infty;\ -6 ]$$
$$\left\{\begin{matrix} \frac{6-3x}{4+(9-2x)^2}\geq0\\ 5-8x\leq23-5x \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} 6-3x\geq0\\ -8x+5x\leq23-5 \end{matrix}\right.\Leftrightarrow\left\{\begin{matrix} x\leq2\\ x\geq-6 \end{matrix}\right.\Rightarrow x\in[-6;2]$$
Задание 13
При проведении химической реакции в растворе образуется нерастворимый осадок. Наблюдения показали, что каждую минуту образуется $$0,5$$ г осадка. Найдите массу осадка (в граммах) в растворе спустя $$8$$ минут после начала реакции.
Задание 14
В окружности с центром в точке $$O$$ проведены диаметры $$AD$$ и $$BC$$, угол $$OAB$$ равен $$25^\circ$$. Найдите градусную меру угла $$OCD$$.
Вписанные углы ВСD и ВАD опираются на одну и ту же дугу окружности, поэтому они равны. Тем самым, угол $$OCD=25^{\circ}.$$
Задание 15
В равнобедренном треугольнике боковая сторона равна $$47$$, основание — $$47\sqrt{3}$$, а угол, лежащий напротив основания, равен $$150^\circ$$. Найдите площадь треугольника.
$$S=\frac{1}{2}\cdot a^2\cdot\sin\alpha=\frac{1}{2}\cdot47^2\cdot\sin150^{\circ}=\frac{47^2}{4}=552,25$$
Задание 16
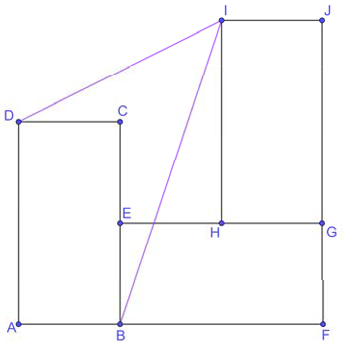
Пусть $$DC=EB=HG=x; AD=EG=IH=y.$$ Тогда $$EH=EG-HG=y-x.$$ Пусть $$DC\cap IH=L.$$
Тогда $$CL=EH=y-x,$$ но $$DL=x+y-x=y.$$
Тогда $$DI=\sqrt{DL^2+LI^2}=\sqrt{y^2+x^2}$$
$$(CE=y-x=HL\Rightarrow LI=y-(y-x)=x)$$
$$DB=\sqrt{x^2+y^2}.$$ Получим $$DI=DB.$$
При этом $$\Delta ADB=\Delta DLI.$$ Тогда $$\angle ADB=\angle IDL.$$
Следовательно, $$\angle IDB=\angle ADC=90^{\circ}\Rightarrow\angle BID=\frac{90^{\circ}}{2}=45^{\circ}.$$
Задание 17
Какие из следующих утверждений верны? Если верных утверждений несколько, запишите их номера в порядке возрастания без пробелов, запятых и других разделительных символов.
- В любую равнобедренную трапецию можно вписать окружность.
- Диагональ параллелограмма делит его углы пополам.
- Площадь прямоугольного треугольника равна половине произведения его катетов.
1) неверно, так как в трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон
2) неверно, так как для этого требуется условие равенства всех сторон параллелограмма.
3) верно
Задание 19
Моторная лодка прошла $$36$$ км по течению реки и вернулась обратно, потратив на весь путь $$5$$ часов. Скорость течения реки равна $$3$$ км/ч. Найдите скорость лодки в неподвижной воде.
Пусть х км/ч - собственная скорость лодки, тогда х+3 км/ч - скорость лодки по течению и $$t_{1}=\frac{36}{x+3}$$ часов - время лодки по течению; х-3 км/ч - скорость лодки против течения и $$t_{2}=\frac{36}{x-3}$$ часов - время против течения. Суммарное время движения составляет 5 часов, то есть: $$t_{1}+t_{2}=5$$, получаем:
$$\frac{36}{x+3}+\frac{36}{x-3}=5|*(x-3)(x+3)\Leftrightarrow$$$$36x-108+36x+108=5x^{2}-45\Leftrightarrow$$$$5x^{2}-72x-45=0\Rightarrow$$$$D=5184+900=6084=78^{2}\Rightarrow$$$$x_{1}=\frac{72+78}{10}=15, x_{2}<0$$, то есть собственная скорость лодки составляла 15 км/ч
Задание 20
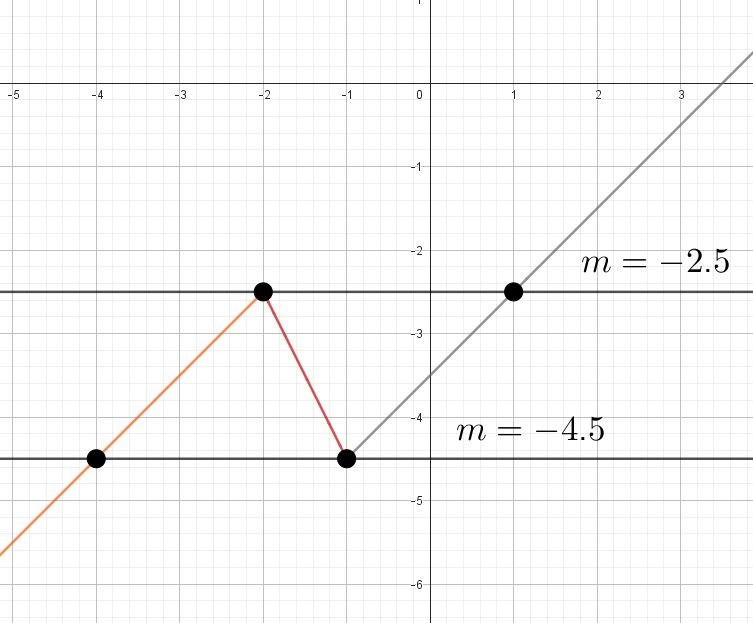
Постройте график функции $$y = \left\{\begin{aligned} x - 0{,}5, & x < -2; \\ -2x - 6{,}5, & -2 \leq x \leq -1; \\ x - 3{,}5, & x > -1 \end{aligned}\right.$$ Определите, при каких значениях $$a$$ прямая $$y = a$$ имеет с графиком этой функции ровно две общие точки.
Для построения прямой достаточно двух точек.
$$x=-3: y=-3-0,5=-3,5$$
$$x=-2: y=-2-0,5=-2,5$$ (пустая, так как $$x<-2$$)
$$x=-2: y=-2\cdot(-2)-6,5=-2,5$$ (закрашенная, так как тут $$x\geq-2$$)
В итоге пустая и закрашенная дадут закрашенную.
$$x=-1: y=(-2)\cdot(-1)-6,5=-4,5.$$
$$x=-1: y=-1-3,5=-4,5.$$
$$x=0: y=0-3,5=-3,5.$$
Задание 21
Дан правильный шестиугольник. Докажите, что если последовательно соединить отрезками середины его сторон, то получится правильный шестиугольник.
Рассмотрим треугольники $$ABC$$ и $$BDE.$$
Т.к. стороны правильного шестиугольника равны, то и $$CA=AB=BD=DE, \angle A=\angle D,$$ т.к. углы правильного шестиугольника тоже равны. Следовательно, данные треугольники равны (по первому признаку равенства треугольников).
Тогда $$BC=BE.$$ Углы $$\angle BCA=\angle CBA=\angle EBD=\angle BED$$ (по свойству равнобедренного треугольника). Следовательно внутренние углы $$\angle С=\angle B=\angle E.$$
Данные выкладки справедливы для любой пары треугольников, следовательно все стороны внутреннего шестиугольника равны и все внутренние углы равны. Это означает, что внутренний шестиугольник - правильный (по определению).