ОГЭ математика 2022. Разбор варианта Алекса Ларина № 305.
Больше разборов на моем ютуб-канале
Задание 1-5
Метро
На рисунке изображена схема метро города N. Станция Ветреная расположена между станциями Центральная и Дальняя. Если ехать по кольцевой линии (она имеет форму окружности), то можно последовательно попасть на станции Центральная, Быстрая, Утренняя, Птичья и Весёлая. Радужная ветка включает в себя станции Быстрая, Смородиновая, Хоккейная и Звёздная. Всего в метрополитене города N есть три станции, от которых тоннель ведёт только в одну сторону — это станции Дальняя, Верхняя и Звёздная. Антон живёт недалеко от станции Надежда.
1. Для станций, указанных в таблице, определите, какими цифрами они обозначены на схеме. В ответе запишите последовательность четырёх цифр без пробелов, запятых и других разделительных символов.
| Станции | Весёлая | Ветреная | Звёздная | Птичья |
| Цифры |
2. Бригада меняет рельсы на участке между станциями Надежда и Верхняя протяжённостью 12,4 км. Работы начались в понедельник. Каждый рабочий день бригада меняла по 400 метров рельсов. По субботам и воскресеньям замена рельсов не осуществлялась, но проезд был закрыт до конца всего ремонта. Сколько дней был закрыт проезд между указанными станциями?
3. Территория, находящаяся внутри кольцевой линии, называется Центральным городским районом. Найдите его площадь S (в км2), если длина кольцевой ветки равна 40 км. В ответе укажите значение выражения $$S\cdot \pi$$.
4. Найдите расстояние (в км) между станциями Смородиновая и Хоккейная, если длина Радужной ветки равна 17 км, расстояние от Звёздной до Смородиновой равно 10 км, а от Быстрой до Хоккейной — 12 км. Все расстояния даны по железной дороге.
5. Школьник Антон в среднем в месяц совершает 45 поездок в метро. Для оплаты поездок можно покупать различные карточки. Стоимость одной поездки для разных видов карточек различна. По истечении месяца Антон уедет из города и неиспользованные карточки обнуляются. Во сколько рублей обойдётся самый дешёвый вариант?
| Количество поездок | Стоимость карточки | Дополнительные условия |
| 1 | 40 | школьникам скидка 15% |
| 10 | 370 | школьникам скидка 10% |
| 30 | 1050 | школьникам скидка 10% |
| 50 | 1600 | нет |
| не ограничено | 2000 | нет |
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 8
Найдите значение выражения $$(\sqrt{12} - \sqrt{3}) \cdot \sqrt{3}$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 10
Из $$600$$ клавиатур для компьютера в среднем $$12$$ неисправны. Какова вероятность того, что случайно выбранная клавиатура исправна?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 11
Ниже представлены графики функций вида $$y = f(x) = kx + b$$ и значения коэффициентов $$k$$ и $$b$$. Установите соответствие между графиками функций и значениями коэффициентов $$k$$ и $$b$$. В ответе укажите последовательность цифр, соответствующих А, Б, В, без пробелов, запятых и других разделительных символов.
ГРАФИКИ
КОЭФФИЦИЕНТЫ
А. $$k<0$$, $$b<0$$
Б. $$k<0$$, $$b>0$$
В. $$k>0$$, $$b<0$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 12
Площадь ромба можно вычислить по формуле $$S = \frac{1}{2}d_1 d_2$$, где $$d_1$$, $$d_2$$ — диагонали ромба. Пользуясь этой формулой, найдите диагональ $$d_1$$, если диагональ $$d_2 = 30$$, а площадь ромба $$180$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 13
Укажите решение системы неравенств:
$$\left\{\begin{aligned} -12 + 3x 0 \\ 9 - 4x > -23 \end{aligned}\right.$$
1) $$( -\infty;\ 8 )$$
2) $$( -\infty;\ 4 )$$
3) $$( 4;\ 8 )$$
4) $$( 4;\ +\infty )$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 14
Тренер посоветовал Андрею в первый день занятий провести на беговой дорожке $$15$$ минут, а на каждом следующем занятии увеличивать время, проведённое на беговой дорожке, на $$7$$ минут. За сколько занятий Андрей проведёт на беговой дорожке в общей сложности $$2$$ часа $$25$$ минут, если будет следовать советам тренера?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 15
Точка $$O$$ — центр окружности, на которой лежат точки $$S$$, $$T$$ и $$V$$, таким образом, что $$OSTV$$ — ромб. Найдите угол $$STV$$. Ответ дайте в градусах.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 16
Точка $$O$$ — центр окружности, на которой отмечены три различные точки $$A$$, $$B$$, $$C$$. Известно, что $$\angle ACB = 25^\circ$$. Найдите величину угла $$AOB$$ (в градусах).
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 17
В треугольнике $$ABC$$ отмечены середины $$M$$ и $$N$$ сторон $$BC$$ и $$AC$$ соответственно. Площадь треугольника $$CNM$$ равна $$76$$. Найдите площадь четырёхугольника $$ABMN$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 19
Какие из следующих утверждений верны? Если верных утверждений несколько, запишите их номера в порядке возрастания без пробелов, запятых и других разделительных символов.
- Боковые стороны любой трапеции равны.
- Площадь ромба равна произведению двух его смежных сторон на синус угла между ними.
- Всякий равнобедренный треугольник является остроугольным
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 21
Из $$A$$ в $$B$$ одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого автомобилиста на $$11$$ км/ч, а вторую половину пути проехал со скоростью $$66$$ км/ч, в результате чего прибыл в $$B$$ одновременно с первым автомобилистом. Найдите скорость (в км/ч) первого автомобилиста, если известно, что она больше $$40$$ км/ч.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Пусть х км/ч - скорость первого, тогда х-11 км/ч - скорость второго на первой половине пути. Примем все расстояние за S км. Тогда, $$t_{1}=\frac{S}{x}$$ часов - время первого, $$t_{2}=\frac{0,5S}{x-11}+\frac{0,5S}{66}$$ часов - время второго. Велосипедисты прибыли одновременно, следовательно: $$\frac{S}{x}=\frac{0,5S}{x-11}+\frac{0,5S}{66}|:S\Leftrightarrow$$$$\frac{1}{x}=\frac{0,5}{x-11}+\frac{0,5}{66}|*66x(x-11)\Leftrightarrow$$$$66(x-11)=33x+0,5x(x-11)|*2\Leftrightarrow$$$$132x-132*11=66x+x^{2}-11x\Leftrightarrow$$$$x^{2}-77x+1452=0\Rightarrow$$$$\left\{\begin{matrix}x_{1}+x_{2}=77\\x_{1}*x_{2}=1452\end{matrix}\right.\Rightarrow$$$$\left[\begin{matrix}x_{1}=33\\x_{2}=44\end{matrix}\right.$$, скорость должна быть более 40 км/ч, то есть 44 км/ч
Задание 22
Постройте график функции $$y = |x + 1| - |x - 1|$$. Определите, при каких значениях $$a$$ прямая $$y = ax$$ имеет с графиком ровно одну общую точку.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 23
В параллелограмме $$ABCD$$ проведены высоты $$BE$$ и $$BF$$ к сторонам $$AD$$ и $$CD$$ соответственно. Докажите, что треугольник $$ABE$$ подобен треугольнику $$CBF$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


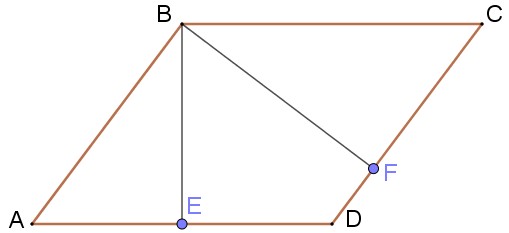
- $$BE\perp AD \Rightarrow \angle BEA=90^\circ$$
- $$BF\perp DC \Rightarrow \angle BFC=90^\circ\Rightarrow$$ $$\angle BEA\angle BFC$$
- $$ABCD$$ - параллелограмм, тогда $$\angle BAE=\angle BCF$$
- $$\triangle ABE \sim \triangle CBF$$ по двум углам.