ОГЭ математика 2022. Разбор варианта Алекса Ларина № 298.

Какому из данных промежутков принадлежит число $$\frac{2}{7}$$? В ответе укажите номер правильного варианта ответа.
1) $$[0,1; 0,2]$$
2) $$[0,2; 0,3]$$
3) $$[0,3; 0,4]$$
4) $$[0,4; 0,5]$$

Найдите значение выражения $$\frac{c^2 - ac}{a^2} : \frac{c - a}{a}$$, если $$a = 5$$ и $$c = 26$$.

В коробке $$14$$ пакетиков с чёрным чаем и $$6$$ пакетиков с зелёным чаем. Павел наугад вынимает один пакетик. Какова вероятность того, что это пакетик с зелёным чаем?

Ниже представлены графики функции вида $$y = ax^2 + bx + c$$. Установите соответствие между графиками функций и формулами, которые их задают. В ответе укажите последовательность цифр, соответствующих А, Б, В, Г, без пробелов, запятых и других разделительных символов.

ГРАФИКИ

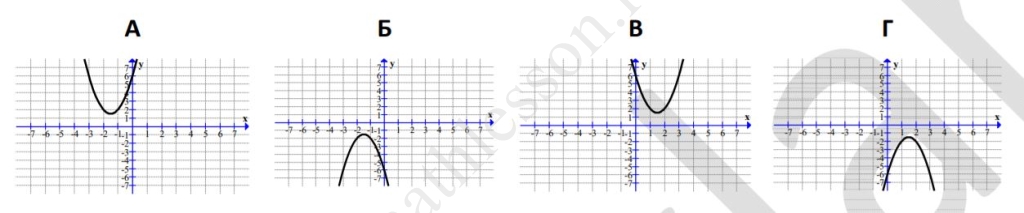
ФОРМУЛЫ
1) $$y = -2x^2 + 6x - 6$$
2) $$y = -2x^2 - 6x - 6$$
3) $$y = 2x^2 + 6x + 6$$
4) $$y = 2x^2 - 6x + 6$$

Закон Джоуля–Ленца можно записать в виде $$Q = I^2 R t$$, где $$Q$$ — количество теплоты (в джоулях), $$I$$ — сила тока (в амперах), $$R$$ — сопротивление цепи (в омах), а $$t$$ — время (в секундах). Пользуясь этой формулой, найдите время $$t$$ (в секундах), если $$Q = 1521$$ Дж, $$I = 6,5$$ А, $$R = 9$$ Ом.

При каких значениях $$x$$ значение выражения $$9x + 7$$ меньше значения выражения $$8x - 3$$? В ответе укажите номер правильного варианта ответа.
1) $$( 4;\ +\infty )$$
2) $$( -\infty;\ 4 )$$
3) $$( -10;\ +\infty )$$
4) $$( -\infty;\ -10 )$$

Ваня, Миша, Алик и Вадим ловили рыбу. Оказалось, что количества рыб, пойманных каждым из них, образуют в указанном порядке арифметическую прогрессию. Если бы Алик поймал столько же рыб, сколько Вадим, а Вадим поймал бы на $$12$$ рыб больше, то количества рыб, пойманных юношами, образовали бы в том же порядке геометрическую прогрессию. Сколько рыб поймал Миша?

Найдите меньший угол равнобедренной трапеции, если два её угла относятся как $$2:3$$.

В параллелограмм вписана окружность. Найдите периметр параллелограмма, если одна из его сторон равна $$12$$.

Найдите площадь треугольника с длинами сторон $$86$$, $$122$$ и $$136$$.

На рисунке изображён четырёхугольник. Используя рисунок, найдите его площадь, если известно, что $$AD = 2$$.

Какие из следующих утверждений верны? Если верных утверждений несколько, запишите их номера в порядке возрастания без пробелов, запятых и других символов между ними.

1. Основания любой трапеции параллельны.
2. Тангенс любого острого угла меньше единицы.
3. Сумма углов любого треугольника равна $$360^{\circ}$$ градусам

Смешав $$60$$ - процентный и $$30$$ - процентный растворы кислоты и добавив $$5$$ кг чистой воды, получили $$20$$ - процентный раствор кислоты. Если бы вместо $$5$$ кг воды добавили $$5$$ кг $$90$$ - процентного раствора той же кислоты, то получили бы $$70$$ - процентный раствор кислоты. Сколько килограммов $$60$$ - процентного раствора использовали для получения смеси?

На стороне $$AC$$ треугольника $$ABC$$ отмечены точки $$D$$ и $$E$$ так, что $$AD=CE$$. Докажите, что если $$BD=BE$$, то $$AB=BC$$.