ОГЭ математика 2022. Разбор варианта Алекса Ларина № 291.
Больше разборов на моем ютуб-канале
Задание 9
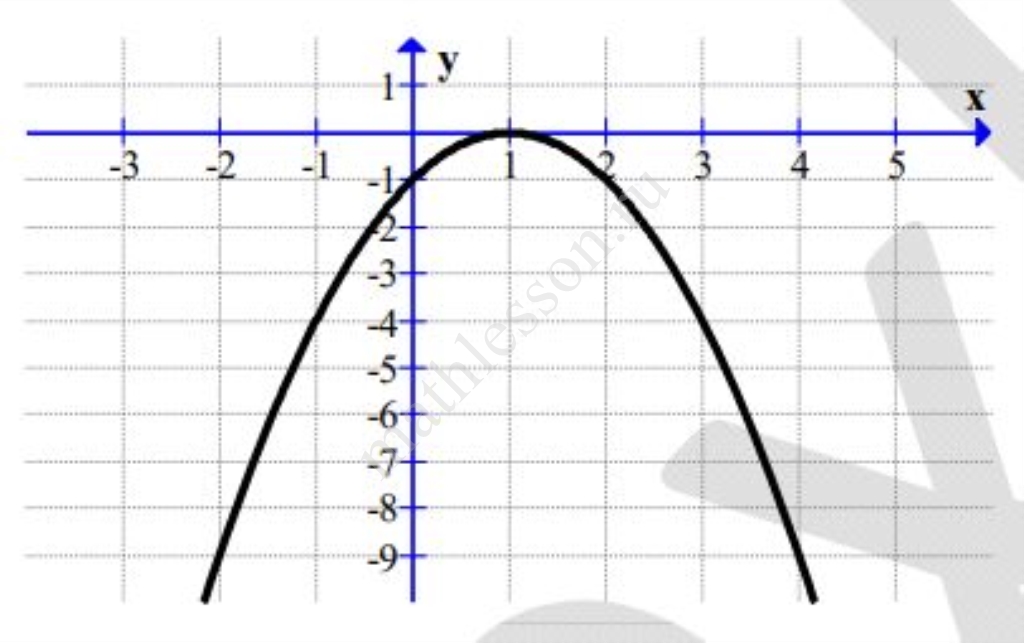
На рисунке изображён график функции $$y = ax^2 + bx + c$$. Установите соответствие между утверждениями и промежутками, на которых эти утверждения выполняются. В ответе укажите последовательность цифр, соответствующих А, Б, без пробелов, запятых и других разделительных символов.
УТВЕРЖДЕНИЯ
А) Функция убывает на промежутке
Б) Функция возрастает на промежутке
ПРОМЕЖУТКИ
1) $$[1; 2]$$
2) $$[0; 2]$$
3) $$[-1; 0]$$
4) $$[-2; 3]$$
В таблице под каждой буквой укажите соответствующий номер.
| А | Б |
Задание 10
Чтобы перевести значение температуры по шкале Цельсия ($$t^\circ\text{C}$$) в шкалу Фаренгейта ($$t^\circ\text{F}$$), пользуются формулой $$F = 1{,}8C + 32$$, где $$C$$ — градусы Цельсия, $$F$$ — градусы Фаренгейта. Какая температура по шкале Фаренгейта соответствует $$111^\circ$$ по шкале Цельсия?
Задание 16
Какие из следующих утверждений верны? Если верных утверждений несколько, запишите их номера в порядке возрастания без пробелов, запятых и других символов между ними.
- Любые три различные прямые имеют не более одной общей точки.
- Если угол равен $$120^{\circ}$$, то смежный с ним равен .
- Если расстояние от точки до прямой больше $$3$$, то и длина любой наклонной, проведённой из данной точки к прямой, больше $$3$$.