ОГЭ математика 2021. Разбор варианта Алекса Ларина № 267.
Больше разборов на моем ютуб-канале
Задание 1-5
Ларинское
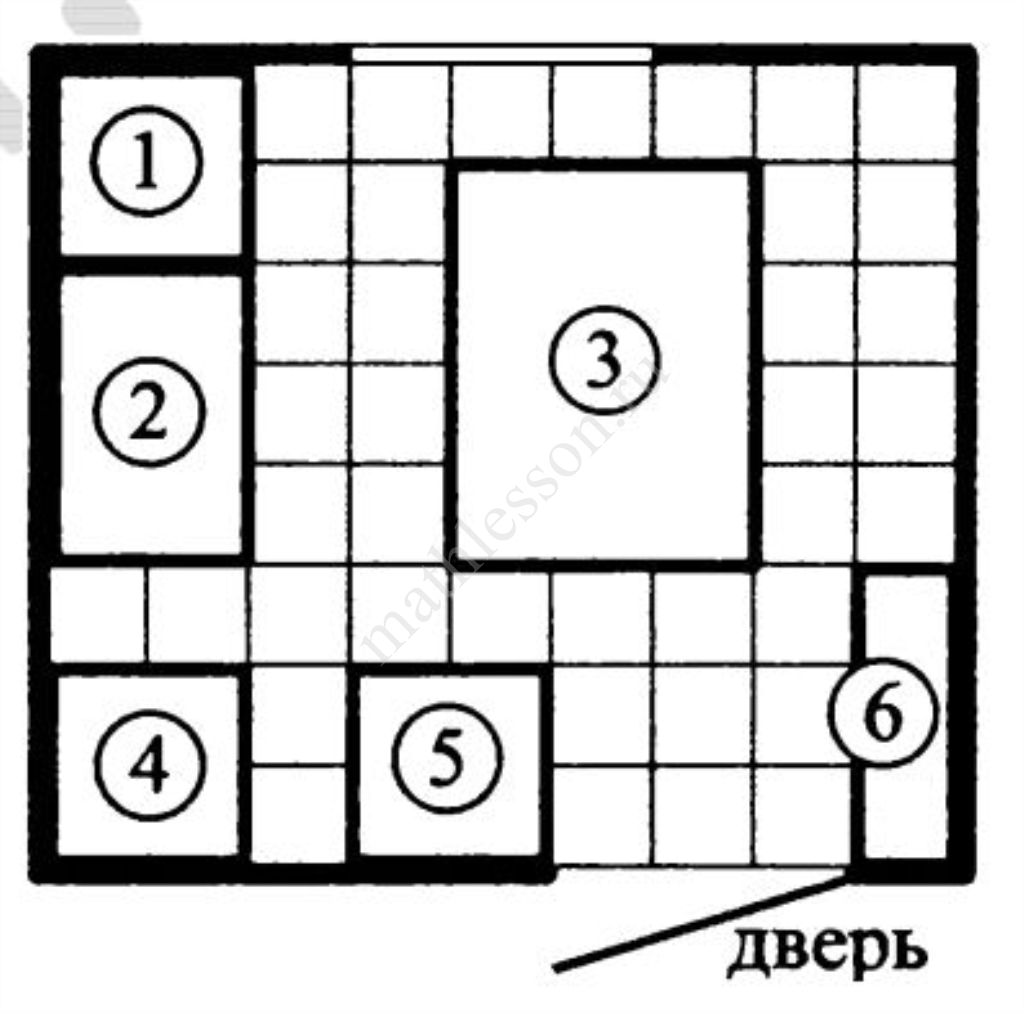
Владелец собирается провести ремонт своей квартиры. На плане (см. выше) изображена будущая расстановка мебели и бытовой техники на кухне после ремонта. Сторона каждой клетки на плане равна 0,4 м. Кухня имеет прямоугольную форму. Единственная дверь кухни деревянная, в стене напротив двери расположено окно. Справа от двери будут поставлены полки для посуды, слева от двери будет холодильник. Слева от холодильника, в углу кухни, предполагается смонтировать раковину. Между раковиной и газовой плитой будет собран буфет, отмеченный на плане цифрой 2. Площадь, занятая буфетом, по плану будет равна 0,96 м2. В центре кухни планируется поставить обеденный стол.
Пол кухни (в том числе там, где будет стоять мебель и бытовая техника) планируется покрыть плиткой в размере 40 см × 40 см. Кроме того, владелец квартиры планирует смонтировать на кухне электрический подогрев пола. Чтобы сэкономить, владелец не станет проводить обогрев под холодильник, газовую плиту, буфет, раковину и полки для посуды, а также на участок площадью 0,32 м2 между буфетом и раковиной.
1. Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в ответе запишите последовательность четырёх цифр без пробелов, запятых и других разделительных символов.
| Объекты | Стол | Холодильник | Газовая плита | Раковина |
| Цифры |
2. Плитка для пола продаётся в упаковках по 5 штук. Сколько упаковок плитки нужно купить, чтобы покрыть пол кухни?
3. Найдите площадь той части кухни, на которой будет смонтирован электрический подогрев пола. Ответ дайте в м2.
4. Найдите расстояние (по прямой) между противоположными углами обеденного стола. Ответ дайте в метрах.
5. Владелец квартиры выбирает холодильник из двух моделей А и Б. Цена холодильников и их среднее суточное потребление электроэнергии указаны в таблице. Цена электроэнергии составляет 4 рубля за кВт∙ч. Обдумав оба варианта, владелец квартиры выбрал модель А. Через сколько лет непрерывной работы экономия от меньшего расхода электроэнергии окупит разницу в цене этих холодильников? Ответ округлите до целого числа.
| Модель | Цена (руб.) | Среднее потребление электроэнергии в сутки (кВт∙ч) |
| А | 34 600 | 0,8 |
| Б | 31 000 | 1,1 |
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 6
Найдите значение выражения $$(\frac{1}{2}+\frac{1}{4})^{-2}:((\sqrt{5}-2)^{2}-4\sqrt{5})^{-1}$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 7
Найдите значение выражения $$\left(\frac{m - n}{m^2 + mn} + \frac{1}{m}\right) : \frac{m}{m + n}$$ при $$m = -0,25$$; $$n = \sqrt{5} - 1$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 8
Решите уравнение: $$x^2 + 4x = 5$$. В ответе запишите корни этого уравнения без пробелов, запятых и других символов между корнями.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 9
В каждой пятой банке кофе согласно условиям акции есть приз. Призы распределены по банкам случайно. Галя покупает банку кофе в надежде выиграть приз. Найдите вероятность того, что Галя не найдёт приз в своей банке.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


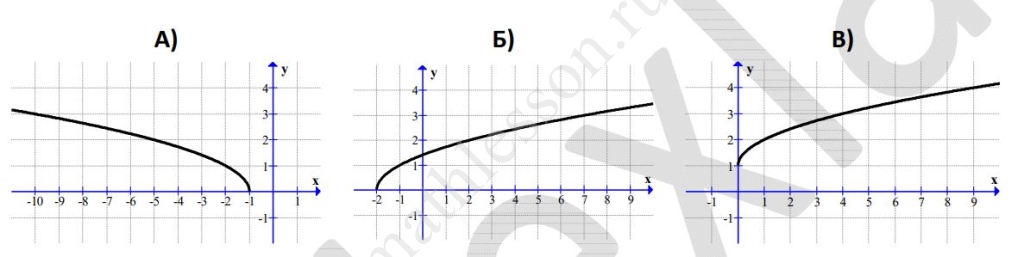
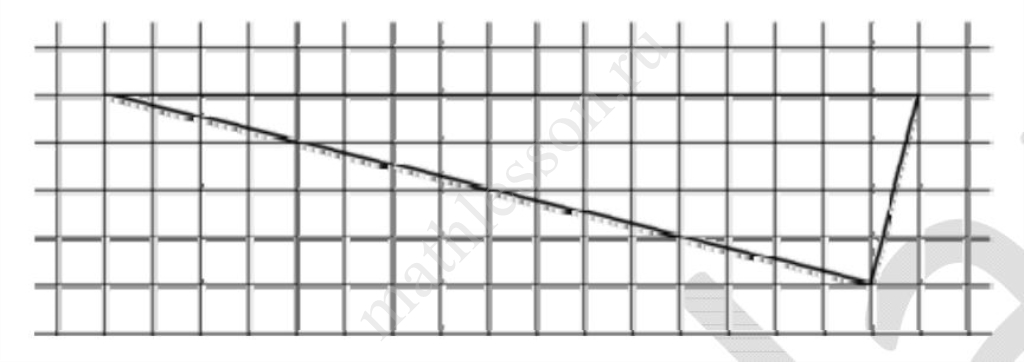
Задание 10
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 11
Площадь четырёхугольника можно вычислить по формуле $$S = \frac{d_1 d_2 \sin \varphi}{2}$$, где $$d_1$$ и $$d_2$$ — длины диагоналей четырёхугольника, $$\varphi$$ — угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали $$d_2$$, если $$d_1 = 6$$, $$\sin \varphi = \frac{1}{12}$$, $$S = 3,75$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 12
Решите неравенство $$\sqrt{3x - 5} \ge 2x - 4$$. В ответе укажите номер правильного варианта ответа:
1) $$\left[\frac{5}{3};\ 3\right]$$
2) $$\left[\frac{7}{4};\ 3\right]$$
3) $$[ 3;\ +\infty )$$
4) $$( -\infty;\ 1 ] \cup \left[\frac{9}{5};\ +\infty\right)$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 13
Рабочие прокладывают тоннель длиной $$500$$ метров, ежедневно увеличивая норму прокладки на одно и то же число метров. Известно, что за первый день рабочие проложили $$3$$ метра тоннеля. Определите, сколько метров тоннеля проложили рабочие в последний день, если вся работа была выполнена за $$10$$ дней.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 14
Найдите больший угол равнобедренной трапеции $$ABCD$$, если диагональ $$AC$$ образует с основанием $$AD$$ и боковой стороной $$AB$$ углы, равные $$36^\circ$$ и $$19^\circ$$ соответственно.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 15
Точка $$O$$ – центр окружности, на которой лежат точки $$A$$, $$B$$ и $$C$$. Известно, что $$\angle ABC = 15^\circ$$ и $$\angle OAB = 8^\circ$$. Найдите градусную меру угла $$BCO$$. Если найденных значений несколько, запишите их в порядке возрастания без пробелов, запятых и других символов между ними.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 16
В трапеции $$ABCD$$ с основаниями $$AD$$ и $$BC$$ известно, что $$AD = 8$$, $$BC = 2$$, а её площадь равна $$35$$. Найдите площадь треугольника $$ABC$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 17
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 18
Какие из следующих утверждений верны? Если верных утверждений несколько, запишите их номера в порядке возрастания без пробелов, запятых и других символов между ними.
- Если расстояние между центрами двух окружностей равно сумме их диаметров, то эти окружности касаются.
- Вписанные углы окружности равны.
- Если вписанный угол равен $$30^{\circ}$$, то дуга окружности, на которую он опирается, равна $$30^{\circ}$$.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 19
Решите систему неравенств: $$\left\{\begin{aligned} \frac{2 - x}{2 - (3 - x)^2} \ge 0 \\ 6 - 9x \le 31 - 4x \end{aligned}\right.$$
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 20
Два оператора, работая вместе, могут набрать текст газеты объявлений за $$8$$ ч. Если первый оператор будет работать $$3$$ ч, а второй $$12$$ ч, то они выполнят только $$75 \%$$ всей работы. За сколько часов может набрать весь текст первый оператор, работая отдельно?
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 21
Постройте график функции $$y = \left\{ \begin{aligned} x^2 + 2x + 3,&\ x \ge -3 \\ x + 9,&\ x < -3 \end{aligned} \right.$$ и определите, при каких значениях $$a$$ прямая $$y = a$$ имеет с графиком функции ровно две общие точки.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 22
Окружность пересекает стороны $$AB$$ и $$AC$$ треугольника $$ABC$$ в точках $$K$$ и $$P$$ соответственно и проходит через вершины $$B$$ и $$C$$. Найдите длину отрезка $$KP$$, если $$AP=34$$, а сторона $$AC$$ в $$2$$ раза больше стороны $$BC$$ .
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 23
В параллелограмме $$ABCD$$ точка $$E$$ — середина стороны $$AB$$ . Известно, что $$EC=ED$$. Докажите, что данный параллелограмм — прямоугольник.
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!